Rovnoběžníku 65954
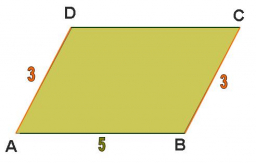
V rovnoběžníku ABCD platí AB = 8, BC = 5, BD = 7 . Vypočtěte velikost úhlu α = ∠DAB (ve stupních).
Správná odpověď:
Tipy na související online kalkulačky
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Čtyřúhelník
Čtyřúhelník ABCD je složen ze dvou pravoúhlých trojúhelníků ABD a BCD. Pro délky stran platí: | AD | = 3cm, | BC | = 12cm, | BD | = 5cm. Kolik centimetrů čtverečních má čtyřúhelník ABCD? Úhly DAB a DBC jsou pravé. - Rovnoramenný 2588
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v - Čtyřúhelník 3262
Sestrojte čtyřúhelník ABCD o rozměrech AB, BC, AC, BD a úhlem d = CDA. - Rovnoramenného 48073
Vypočítejte obsah rovnoramenného lichoběžníku ABCD, pokud a = 14 cm, c = 8 cm a velikost úhlu DAB je 52°. - Rovnoramenný 15
Rovnoramenný trojúhelník má velikost úhlů u základny alfa =beta=34 stupnů 34 minut. Vypočtěte ve stupních a minutách velikost úhlu u zbývajícího vrcholu trojúhelníku. - Obsah trojúhelníku
Vypočtěte velikost ramene b lichoběžníku ABCD, pokud a = 12 cm, c = 4 cm, d(AC)= d(BC) a obsah S(trojúhelníku ABC) = 9 cm čtverečních. - Rovnoběžník
V rovnoběžníku ABCD je strana AB třikrát delší než strana BC obvod rovnoběžníku je 20 cm. Urči délky stran rovnoběžníku.
