PRT
Jaký obvod má pravoúhlý trojúhelník s odvěsnami 10 cm a 30 cm?
Správná odpověď:
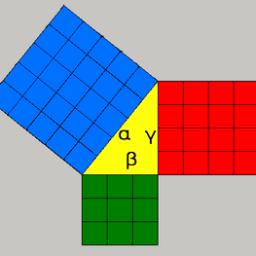
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Vypočtěte 18
 Vypočtěte obvod kružnice opsané pravoúhlého trojúhelníku s odvěsnami o delce 10cm a 15cm.
Vypočtěte obvod kružnice opsané pravoúhlého trojúhelníku s odvěsnami o delce 10cm a 15cm. - Kolmý trojboký hranol
 Podstavou kolmého trojbokého hranolu je pravoúhlý trojúhelník s odvěsnami 4,5cm a 6cm. Jaký je povrch tohoto hranolu, pokud je jeho objem 54 cm³?
Podstavou kolmého trojbokého hranolu je pravoúhlý trojúhelník s odvěsnami 4,5cm a 6cm. Jaký je povrch tohoto hranolu, pokud je jeho objem 54 cm³? - Trojúhelníku 6950
 Jaký je objem trojbokého hranolu s podstavou pravoúhlého trojúhelníku s odvěsnami 6 dm a 8 dm a přeponou 10 dm a výška hranolu je 40 dm?
Jaký je objem trojbokého hranolu s podstavou pravoúhlého trojúhelníku s odvěsnami 6 dm a 8 dm a přeponou 10 dm a výška hranolu je 40 dm? - Trojúhelníku 31991
 Vypočítejte objem a povrch hranolu, jehož výška je 16cm a podstava má tvar pravoúhlého trojúhelníku s odvěsnami 5cm a 12cm a přeponou 13cm.
Vypočítejte objem a povrch hranolu, jehož výška je 16cm a podstava má tvar pravoúhlého trojúhelníku s odvěsnami 5cm a 12cm a přeponou 13cm.
- Rovnoramenný 5711
 Rovnoramenný trojúhelník s délkou základny 32 cm má obsah 480 cm². Jaký má obvod?
Rovnoramenný trojúhelník s délkou základny 32 cm má obsah 480 cm². Jaký má obvod? - Výška hranolu
 Jaká je výška hranolu s podstavou pravoúhlého trojúhelníku s odvěsnami 6 cm a 9 cm? Přepona má délku 10,8 cm. Objem hranolu je 58 cm³. Vypočítejte jeho povrch.
Jaká je výška hranolu s podstavou pravoúhlého trojúhelníku s odvěsnami 6 cm a 9 cm? Přepona má délku 10,8 cm. Objem hranolu je 58 cm³. Vypočítejte jeho povrch. - RR lichoběžník v2
 Základny RR (rovnoramenného) lichoběžníku měří 15 cm a 2 cm, jeho obvod je 38 cm. Jaký obsah má lichoběžník?
Základny RR (rovnoramenného) lichoběžníku měří 15 cm a 2 cm, jeho obvod je 38 cm. Jaký obsah má lichoběžník? - Podstavu
 Podstavu kolmého hranolu tvoří pravoúhlý trojúhelník s odvěsnami délky 30 cm a 40 cm. Tento hranol má stejný objem jako krychle o hraně délky 3 dm. Urči jeho výšku v cm
Podstavu kolmého hranolu tvoří pravoúhlý trojúhelník s odvěsnami délky 30 cm a 40 cm. Tento hranol má stejný objem jako krychle o hraně délky 3 dm. Urči jeho výšku v cm - Zaokrouhlete 64084
 Pravoúhlému trojúhelníku ABC s odvěsnami 5 cm a 12 cm je popsána kružnice k. Vypočítejte délku kružnice k v centimetrech. Při výpočtu použijte π = 3, 14 a výsledek zaokrouhlete na desetiny.
Pravoúhlému trojúhelníku ABC s odvěsnami 5 cm a 12 cm je popsána kružnice k. Vypočítejte délku kružnice k v centimetrech. Při výpočtu použijte π = 3, 14 a výsledek zaokrouhlete na desetiny.
- Rotace
 Pravoúhlý trojúhelník s odvěsnami 9 cm a 10 cm rotuje kolem delší odvěsny. Vypočítejte objem a povrch takto vzniklého kužele.
Pravoúhlý trojúhelník s odvěsnami 9 cm a 10 cm rotuje kolem delší odvěsny. Vypočítejte objem a povrch takto vzniklého kužele. - Rovnoramenného 9881
 Obsah rovnoramenného pravoúhlého trojúhelníku je 32cm čtverečních. Jaký je jeho obvod?
Obsah rovnoramenného pravoúhlého trojúhelníku je 32cm čtverečních. Jaký je jeho obvod? - Trojúhelníku 20383
 Do 10 l kbelíku jsme hodili hranol s podstavou pravoúhlého trojúhelníku s odvěsnami 15×10 cm a výškou hranolu 1,5 dm. O kolik se zvýšil objem v kbelíku?
Do 10 l kbelíku jsme hodili hranol s podstavou pravoúhlého trojúhelníku s odvěsnami 15×10 cm a výškou hranolu 1,5 dm. O kolik se zvýšil objem v kbelíku? - Kružnice opsaná
 Poloměr kružnice opsané pravoúhlému trojúhelníku s odvěsnou dlouhou 6 cm, je 5 cm. Vypočítej obvod tohoto trojúhelníku.
Poloměr kružnice opsané pravoúhlému trojúhelníku s odvěsnou dlouhou 6 cm, je 5 cm. Vypočítej obvod tohoto trojúhelníku. - Svislý
 Svislý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikne ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3cm a 4cm. Výška hranolu je 8 cm. Jaký je objem šestib
Svislý šestiboký hranol byl vytvořen opracováním krychle o hraně délky 8 cm. Podstava hranolu vznikne ze čtvercové stěny původní krychle oddělením 4 shodných pravoúhlých trojúhelníků s odvěsnami délek 3cm a 4cm. Výška hranolu je 8 cm. Jaký je objem šestib
- Úhlopříčky
 Úhlopříčky kosočtverce EFGH mají délky v poměru 1:2. Jaký je obvod kosočtverce, jestliže má delší z úhlopříček délku 8cm?
Úhlopříčky kosočtverce EFGH mají délky v poměru 1:2. Jaký je obvod kosočtverce, jestliže má delší z úhlopříček délku 8cm? - Pravoúhlý - proměna
 Z pravoúhlého trojúhelníku s odvěsnami 12 cm a 20 cm jsme sestrojili čtverec se stejným obsahem jako trojúhelník. Jak dlouhá bude strana čtverce?
Z pravoúhlého trojúhelníku s odvěsnami 12 cm a 20 cm jsme sestrojili čtverec se stejným obsahem jako trojúhelník. Jak dlouhá bude strana čtverce? - Trojúhelníku 83265
 Vypočítejte obsah pravoúhlého trojúhelníku ABC s odvěsnami a=15cm, b=1,7dm.
Vypočítejte obsah pravoúhlého trojúhelníku ABC s odvěsnami a=15cm, b=1,7dm.
