Stožár
Stožár vysoký 32 metrů byl větrem zlomen tak, že se jeho vrchol dotýká země 16 metrů od paty stožáru. Ještě stojící část stožáru, ulomená část a země vytvářejí pravoúhlý trojúhelník. V jaké výšce byl stožár zlomen?
Správná odpověď:

Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Bambus
 Bambus vysoký 32 stop byl v určité výšce zlomený větrem tak, že se vrchol bambusu doktol země ve vzdálenosti 16 stop od kmene. V jaké výši od země byl bambus zlomený?
Bambus vysoký 32 stop byl v určité výšce zlomený větrem tak, že se vrchol bambusu doktol země ve vzdálenosti 16 stop od kmene. V jaké výši od země byl bambus zlomený? - Vichřice
 Vichřice nalomila svisle rostoucí smrk ve výšce 8 metrů nd zemí. Vrchol dopadl na zem 6 metrů od paty smrku. Určete původní výšku smrku.
Vichřice nalomila svisle rostoucí smrk ve výšce 8 metrů nd zemí. Vrchol dopadl na zem 6 metrů od paty smrku. Určete původní výšku smrku. - Stožár 6
 Stožár je vysoký 190m a je uchycen šesti lány která jsou ukotvena v zemi ve vzdálenosti 20m od paty stožáru. kolik metrů lana bylo potreba?
Stožár je vysoký 190m a je uchycen šesti lány která jsou ukotvena v zemi ve vzdálenosti 20m od paty stožáru. kolik metrů lana bylo potreba? - Zlomený smrk
 Patnactimetrovému smrku ulomila mohutná vichřice vršek tak,že zůstal viset podél zbytku jeho kmene. Vzdálenost tohoto visicího vršku od země byla 4,6 m. V jaké výšce byl kmen smrku zlomen?
Patnactimetrovému smrku ulomila mohutná vichřice vršek tak,že zůstal viset podél zbytku jeho kmene. Vzdálenost tohoto visicího vršku od země byla 4,6 m. V jaké výšce byl kmen smrku zlomen?
- Strom
 Při vichřici se zlomil strom ve výšce 3 metrů. Jeho vrchol dopadl 4,5 m od stromu. Jak vysoký byl strom?
Při vichřici se zlomil strom ve výšce 3 metrů. Jeho vrchol dopadl 4,5 m od stromu. Jak vysoký byl strom? - Strom 5
 Strom je zlomen ve výšce 4 metry nad zemí a vršek stromu se dotýká země ve vzdálenosti 5 od kmene. Vypočti původní výšku stromu.
Strom je zlomen ve výšce 4 metry nad zemí a vršek stromu se dotýká země ve vzdálenosti 5 od kmene. Vypočti původní výšku stromu. - Televizní 2
 Televizní vysílač vysoký 108 m je ukotven ve 2/3 své výšky (od země) třemi stejně dlouhými lany. Kolik metrů lana je třeba na ukotvení, je-li zapuštěno ve vzdálenosti 54 m od paty stožáru a počítáme ještě 10% délky lan na ukotvení navíc?
Televizní vysílač vysoký 108 m je ukotven ve 2/3 své výšky (od země) třemi stejně dlouhými lany. Kolik metrů lana je třeba na ukotvení, je-li zapuštěno ve vzdálenosti 54 m od paty stožáru a počítáme ještě 10% délky lan na ukotvení navíc? - Sloup
 Kolmý sloup vysoký 6 m se zlomil a jeho špička dopadla 3,2 m od paty sloupu. V jaké výšce nad zemí se sloup zlomil?
Kolmý sloup vysoký 6 m se zlomil a jeho špička dopadla 3,2 m od paty sloupu. V jaké výšce nad zemí se sloup zlomil? - Strom 2
 Strom byl vysoký 35 m. Strom se zlomil ve výšce 10 m nad zemí. Vršek ale neodpadl, jen se vyvrátil na zem. Jak daleko od paty stromu ležela jeho špička?
Strom byl vysoký 35 m. Strom se zlomil ve výšce 10 m nad zemí. Vršek ale neodpadl, jen se vyvrátil na zem. Jak daleko od paty stromu ležela jeho špička?
- Tři geodeti
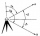 Tři geodeti mají za úkol změřit výšku stožáru stojícího na rovné pláni. První měřič stojící 100 m od stožáru změřil výškový úhel (a), druhý vzdálený 200 m od stožáru změřil výškový úhel (b) a třetí ze vzdálenosti 300 m od stožáru změřil výškový uhel (c).
Tři geodeti mají za úkol změřit výšku stožáru stojícího na rovné pláni. První měřič stojící 100 m od stožáru změřil výškový úhel (a), druhý vzdálený 200 m od stožáru změřil výškový úhel (b) a třetí ze vzdálenosti 300 m od stožáru změřil výškový uhel (c). - Patnactimetrovému 2
 Patnactimetrovému smrku ulomila mohutná vichřice vršek tak,že zůstal opírat o zem. Vzdálenost tohoto vršku od kmene byla 4,6 m dole. V jaké výšce byl kmen smrku zlomen?
Patnactimetrovému smrku ulomila mohutná vichřice vršek tak,že zůstal opírat o zem. Vzdálenost tohoto vršku od kmene byla 4,6 m dole. V jaké výšce byl kmen smrku zlomen? - Vypočítejte 82693
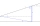 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Smrk
 Jak vysoký byl smrk, který se spilil ve výšce 8m nad zemí a vrcholek dopadl ve vzdálenosti 15m od paty stromu?
Jak vysoký byl smrk, který se spilil ve výšce 8m nad zemí a vrcholek dopadl ve vzdálenosti 15m od paty stromu? - Vzdálenosti 2533
 Stožár vysokého napětí je upevněn lany dlouhými 30 m ve 2/3 výšky stožáru. Jak vysoký je stožár, jsou-li lana ukotvena ve vzdálenosti 15 m od stožáru.
Stožár vysokého napětí je upevněn lany dlouhými 30 m ve 2/3 výšky stožáru. Jak vysoký je stožár, jsou-li lana ukotvena ve vzdálenosti 15 m od stožáru.
- Vzdálen 40911
 V jaké výšce se 15 m žebřík dotýká stěny, je-li jeho dolní konec od stěny vzdálen 2,5 m?
V jaké výšce se 15 m žebřík dotýká stěny, je-li jeho dolní konec od stěny vzdálen 2,5 m? - Žebřík
 Žebřík dlouhý 10 m je opřen o stěnu. Jeho pata je vzdálena od zdi 1,7 m. V jaké výšce se žebřík dotýká stěny?
Žebřík dlouhý 10 m je opřen o stěnu. Jeho pata je vzdálena od zdi 1,7 m. V jaké výšce se žebřík dotýká stěny? - More
 Jak daleko vidět na širém moři z lodního stožáru, jehož vrchol je 14 metrů nad hladinou vody? (Poloměr Země je 6370 km.)
Jak daleko vidět na širém moři z lodního stožáru, jehož vrchol je 14 metrů nad hladinou vody? (Poloměr Země je 6370 km.)
