Klínový řemen
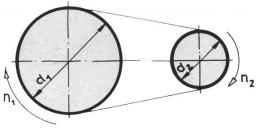
Vypočítejte délku klínového řemene pokud průměr řemenic je:
d1 = 600mm
d2 = 120mm
d = 480mm (vzdálenost os řemenic)
d1 = 600mm
d2 = 120mm
d = 480mm (vzdálenost os řemenic)
Správná odpověď:
Zobrazuji 6 komentářů:
Žák
Výše uvedené řešení vychází z chybného předpokladu, že tečna obou kružnic má stejný sklon ke spojnici středů řemenic jako spojnice průsečíků svislic procházejících středy s kružnicemi. Jinými slovy tečna není rovnoběžná s úsečkou ve výpočtu označenou jako "b". Pochopitelně je tedy chybně určen i úhel "A".
Dr Math
uhel A je uhel tecny vzhledem k spojnici stredu. body dotyku a stredy kruznic S1,S2 formuji pravouhlej lichobeznik, ktery lze rozlozit na obdelnik a pravouhly trojuhelnik. Pravouhlej trojuhelnik ma take uhel A, stranu d = |S1S2| a stranu r1-r2. Tecna je rovnobezna s useckou "b" (dlzka rovne casti remene)...
Proc by take nebyla, kdyz v bodech dotyku je tecna kolma na r1 ale take na r2, tudiz formuje se tam obdelnik o stranach b a r1.
Dejte padnejsi argument.
Proc by take nebyla, kdyz v bodech dotyku je tecna kolma na r1 ale take na r2, tudiz formuje se tam obdelnik o stranach b a r1.
Dejte padnejsi argument.
Dr Math
fuu to dalo namahu nakreslit to. Nicmene nechapu zloute primke s, a aj jinym zlutym primkam. Nemaji zaden smysl. Dulezity je jeno pravouhlej lichobeznik T1T2S2S1. tam je zrejme ze T1S1 je rovnobezne s T2S2. uhel fi = S2PT1 je proste stejny ako uhel spojnici středů řemenic jako spojnice průsečíků svislic procházejících středy s kružnicemi
Žák
No, měl jsem za to, že z obrázku v odkazu je zcela zřejmé, že tečna „t“, pochopitelně procházející body T1, T2, není rovnoběžná s přímkou „s” procházející průsečíky kružnic se svislicemi procházejícími středy. Důkazem budiž třeba to, pominuli již zmiňované analytické řešení, že v pravoúhlém trojúhelníku o stranách d, a, b = |T1T2|, z něhož správně počítáte velikost |T1T2|, musí být příslušný vnitřní úhel pí/6 rad nikoli 0,4636 rad.
Vít
No nevím, také mi to nějak nesedí. Výpočet a použití úhlu A je dost divné. Podle mne ty oblouky jsou 240° a 120°. A výsledek je tedy cca 2214 mm.
4 roky 1 Like
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Řemen
 Vypočítejte délku řemenu na řemenicích s průměry 166 mm a 237 mm při vzdálenosti hřídelů 374 mm.
Vypočítejte délku řemenu na řemenicích s průměry 166 mm a 237 mm při vzdálenosti hřídelů 374 mm. - Lichoběžník
 Lichoběžník ABCD má délku základní a = 120mm, c = 86mm a obsah S = 2575 mm². Vypočítejte výšku lichoběžníku.
Lichoběžník ABCD má délku základní a = 120mm, c = 86mm a obsah S = 2575 mm². Vypočítejte výšku lichoběžníku. - Lichoběžník - výška
 Lichoběžník ABCD má délku základny a = 120 mm, c = 86 mm a plochu A = 2 575 mm². Najděte výšku lichoběžníku.
Lichoběžník ABCD má délku základny a = 120 mm, c = 86 mm a plochu A = 2 575 mm². Najděte výšku lichoběžníku. - Obvod shodných trojúhelníků
 Obvod trojúhelníku MAK je 216 mm, strana a = 81 mm a strana k = 62 mm. Urč délku strany z trojúhelníku OSA, pokud platí, že trojúhelník MAK je shodný s trojúhelníkem OSA.
Obvod trojúhelníku MAK je 216 mm, strana a = 81 mm a strana k = 62 mm. Urč délku strany z trojúhelníku OSA, pokud platí, že trojúhelník MAK je shodný s trojúhelníkem OSA. - Kruhový oblouk
 Vypočítejte délku kruhového oblouku, pokud průměr d = 20cm a úhel alfa = 142°
Vypočítejte délku kruhového oblouku, pokud průměr d = 20cm a úhel alfa = 142° - Cu drát 2
 Na cívce je namotán měděný drát o průměru 1 mm a hmotnosti 350 g. Vypočítejte. Vypočítejte jeho délku, je-li hustota mědi p =8,9 g/cm krychlových.
Na cívce je namotán měděný drát o průměru 1 mm a hmotnosti 350 g. Vypočítejte. Vypočítejte jeho délku, je-li hustota mědi p =8,9 g/cm krychlových. - Statistika výrobních společností
 Náhodný vzorek 8 výrobních společností se vybere z populace výrobních společností. Tržní hodnoty (v milionech randov) těchto osmi výrobních společností jsou: 17 65 117 206 172 181 221 94 Jaká je nejnižší a nejvyšší tržní hodnota? Najděte průměr. Nakreslet
Náhodný vzorek 8 výrobních společností se vybere z populace výrobních společností. Tržní hodnoty (v milionech randov) těchto osmi výrobních společností jsou: 17 65 117 206 172 181 221 94 Jaká je nejnižší a nejvyšší tržní hodnota? Najděte průměr. Nakreslet
