Příklady na povrch kužele - strana 3 z 7
Počet nalezených příkladů: 136
- Rotační telesa
 Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch?
Rotační kužel a rotační válec mají stejný objem 180 cm³ a stejnou výšku v=15cm. Které z těchto dvou těles má větší povrch? - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Správce hradu
 Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří?
Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří? - Rotační kužel
 Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele.
Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele. - Strana kužele
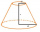 Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°. - Osový řez
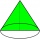 Osový řez kužele je rovnoramenný trojúhelník, v němž je poměr průměru kužele a stěny kužele 2:3. Vypočtěte jeho objem, pokud víte, že jeho plocha je 314 cm čtverečních.
Osový řez kužele je rovnoramenný trojúhelník, v němž je poměr průměru kužele a stěny kužele 2:3. Vypočtěte jeho objem, pokud víte, že jeho plocha je 314 cm čtverečních. - Kužel
 Vypočtěte objem a plochu kužele, jehož výška je 10 cm a v osovém řezu svírá se stěnou kužele úhel 30 stupňů.
Vypočtěte objem a plochu kužele, jehož výška je 10 cm a v osovém řezu svírá se stěnou kužele úhel 30 stupňů. - Zakrytí hromady soli
 Hromada soli byla uložena ve tvaru kužele. Pan Terwilliker ví, že hromada je 20 stop vysoká a 102 stop v obvodu na základně. Jaká plocha kónické plachty (velký kus materiálu) je potřebná k zakrytí hromady?
Hromada soli byla uložena ve tvaru kužele. Pan Terwilliker ví, že hromada je 20 stop vysoká a 102 stop v obvodu na základně. Jaká plocha kónické plachty (velký kus materiálu) je potřebná k zakrytí hromady? - Stínítko na lampe
 Stínidlo na lampu na tvář seříznutého kužele o výšce 20 cm. Horní průměr stínítka je 13 cm, dolní 36 cm a strana svírá s dolním průměrem úhel 60 stupňů. Nejméně kolik látky je potřeba k výrobě tohoto stínítka?
Stínidlo na lampu na tvář seříznutého kužele o výšce 20 cm. Horní průměr stínítka je 13 cm, dolní 36 cm a strana svírá s dolním průměrem úhel 60 stupňů. Nejméně kolik látky je potřeba k výrobě tohoto stínítka? - Kužel 16
 Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy.
Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy. - Kužel - RS trojúhelník
 Povrch kužele je 388,84 cm², osový řez je rovnostranný trojúhelník. Určete objem kužele.
Povrch kužele je 388,84 cm², osový řez je rovnostranný trojúhelník. Určete objem kužele. - Čepice
 Šaškova čepice má tvar rotačního kužele. Vypočítejte kolik papíru je třeba utratit na čepici 50 cm vysokou na obvod hlavy 60 cm.
Šaškova čepice má tvar rotačního kužele. Vypočítejte kolik papíru je třeba utratit na čepici 50 cm vysokou na obvod hlavy 60 cm. - Povrch kužele
 Vypočítejte povrch a objem rotačního kužele, jehož podstava má průměr 6cm, a jeho výška 4cm.
Vypočítejte povrch a objem rotačního kužele, jehož podstava má průměr 6cm, a jeho výška 4cm. - Střecha - krytina
 Střecha hradní věže má tvar kužele o průměru podstavy 12 m a výšce 8m. Kolik eur zaplatíme za pokrytí střechy, pokud 1m čtvereční krytiny stojí 3,5 eura?
Střecha hradní věže má tvar kužele o průměru podstavy 12 m a výšce 8m. Kolik eur zaplatíme za pokrytí střechy, pokud 1m čtvereční krytiny stojí 3,5 eura? - Poměr obsahů
 Poměr obsahu podstavy rotačního kužele k jeho plášti je 3:5. Vypočítejte povrch a objem kužele, pokud jeho výška v = 4 cm.
Poměr obsahu podstavy rotačního kužele k jeho plášti je 3:5. Vypočítejte povrch a objem kužele, pokud jeho výška v = 4 cm. - Komolý kužel
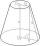 Komolý kužel má poloměr podstav 40cm 10cm a výšku 25cm. Vypočítej jeho povrch a objem.
Komolý kužel má poloměr podstav 40cm 10cm a výšku 25cm. Vypočítej jeho povrch a objem. - Stínítko
 Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem
Stínítko lampy má být tvořeno pláštěm kužele s průměrem podstavy 48cm a stranou 32cm. Vypočítejte, kolik materiálu bude zapotřebí na jeho zhotovení, počítá-li se s 8% odpadem - Odchýlka roviny podstavy
 Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°.
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - Kužel
 Obsah pláště kužele je 4 cm², obsah podstavy kužele je 2 cm². Určete v stupních úhel (odchylku) strany kužele a roviny podstavy kužele. (Strana kužele je úsečka spojující vrchol kužele s libovolným bodem kružnice podstavy. Všechny strany kužele tvoří pláš
Obsah pláště kužele je 4 cm², obsah podstavy kužele je 2 cm². Určete v stupních úhel (odchylku) strany kužele a roviny podstavy kužele. (Strana kužele je úsečka spojující vrchol kužele s libovolným bodem kružnice podstavy. Všechny strany kužele tvoří pláš - Komolý jehlan
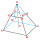 Vypočtěte objem a povrch pravidelného čtyřbokého komolého jehlanu, jestliže a1 = 17 cm, a2 = 5 cm, výška v = 8 cm.
Vypočtěte objem a povrch pravidelného čtyřbokého komolého jehlanu, jestliže a1 = 17 cm, a2 = 5 cm, výška v = 8 cm.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
