Stereometrie - slovní úlohy a příklady - strana 109 z 119
Počet nalezených příkladů: 2379
- Stříška 2
 Kolik plechu je třeba na stříšku, která má tvar pravidelného čtyřbokého jehlanu, jestliže její hrana je dlouhá 2,8 m a výška stříšky je 0,8 m. Počítej 10 % na překryv ( navíc).
Kolik plechu je třeba na stříšku, která má tvar pravidelného čtyřbokého jehlanu, jestliže její hrana je dlouhá 2,8 m a výška stříšky je 0,8 m. Počítej 10 % na překryv ( navíc). - Dva válce
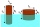 Obdélník o rozměrech 8 cm a 4 cm otočíme o 360º nejprve kolem delší strany, čímž vznikne první těleso. Potom obdélník podobně otočíme kolem kratší strany, čímž vznikne druhé těleso. Určete poměr povrchů prvního a druhého tělesa.
Obdélník o rozměrech 8 cm a 4 cm otočíme o 360º nejprve kolem delší strany, čímž vznikne první těleso. Potom obdélník podobně otočíme kolem kratší strany, čímž vznikne druhé těleso. Určete poměr povrchů prvního a druhého tělesa. - Kolikrát 9
 Kolikrát se zvětší objem koule, jestliže její poloměr se zvětší 2×?
Kolikrát se zvětší objem koule, jestliže její poloměr se zvětší 2×? - Eiffelova věž
 Eiffelova věž v Paříži je 300 metrů vysoká, je zhotovena z oceli. Její hmotnost je 8000 tun. Jak vysoký bude model věže zhotoveného z stejného materiálu, pokud má vážit 2 kg?
Eiffelova věž v Paříži je 300 metrů vysoká, je zhotovena z oceli. Její hmotnost je 8000 tun. Jak vysoký bude model věže zhotoveného z stejného materiálu, pokud má vážit 2 kg? - Trojboký hranol
 Podstava kolmého trojbokého hranolu je pravoúhlý trojúhelník, jehož přepona je 10cm a jedna odvěsna 8cm. Výška hranolu je 75% z obvodu podstavy. Vypočtěte objem a povrch hranolu.
Podstava kolmého trojbokého hranolu je pravoúhlý trojúhelník, jehož přepona je 10cm a jedna odvěsna 8cm. Výška hranolu je 75% z obvodu podstavy. Vypočtěte objem a povrch hranolu. - Kvádr
 Kvádr má povrch 1819 cm², délky jeho hran jsou v poměru 5:1:4. Vypočítej objem kvádru.
Kvádr má povrch 1819 cm², délky jeho hran jsou v poměru 5:1:4. Vypočítej objem kvádru. - Potrubí
 Vodovodní potrubí má průřez 1279 cm². Za hodinu jím proteče 658 m³ vody. Kolik vody proteče potrubím s průřezem 300 cm² za 11 hodin při stejné průtočné rychlosti?
Vodovodní potrubí má průřez 1279 cm². Za hodinu jím proteče 658 m³ vody. Kolik vody proteče potrubím s průřezem 300 cm² za 11 hodin při stejné průtočné rychlosti? - Hmotnost korkového kvádru
 Simon se chlubil, že odnesl korkový kvádr o rozměrech 0,5 m x 0,5 m x 1,2 m . Je to možné, pokud víme, že 1m krychlový korku váží 300 kg a děti od 10 do 15 let mohou nosit nejvýše 5 kg břemeno?
Simon se chlubil, že odnesl korkový kvádr o rozměrech 0,5 m x 0,5 m x 1,2 m . Je to možné, pokud víme, že 1m krychlový korku váží 300 kg a děti od 10 do 15 let mohou nosit nejvýše 5 kg břemeno? - Materiál - textil
 Kolik metrů čtverečních materiálu je třeba na zhotovení dvou shodných kvádrů o rozměrech 6 dm, 8 dm a 12 dm, pokud počítáme 8% materiálu na záhyby? (Zaokrouhlete na dvě desetinná místa. )
Kolik metrů čtverečních materiálu je třeba na zhotovení dvou shodných kvádrů o rozměrech 6 dm, 8 dm a 12 dm, pokud počítáme 8% materiálu na záhyby? (Zaokrouhlete na dvě desetinná místa. ) - Povrch kvádru
 Délky hran kvádru tvoří tři za sebou jdoucí členy GP. Součet délek všech hran je 84 cm a objem kvádru 64 cm³. Určete povrch kvádru.
Délky hran kvádru tvoří tři za sebou jdoucí členy GP. Součet délek všech hran je 84 cm a objem kvádru 64 cm³. Určete povrch kvádru. - Rozhledna 4
 Rozhledna je kryta střechou tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou 8 m a výškou 6 m. 60% krytiny je třeba vyměnit. Kolik m² je třeba zakoupit?
Rozhledna je kryta střechou tvaru pravidelného čtyřbokého jehlanu s podstavnou hranou 8 m a výškou 6 m. 60% krytiny je třeba vyměnit. Kolik m² je třeba zakoupit? - Uhlopříčky
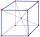 Krychle hrana délky 5cm. Narýsovat ruzne uhlopříčky.
Krychle hrana délky 5cm. Narýsovat ruzne uhlopříčky. - Objem kuželů rotací
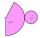 Tenká destička tvaru pravoúhlého trojúhelníku se jednou otočí kolem kratší odvěsny a podruhé kolem delší odvěsny. Rotací se popíší kužely. Mají stejný objem? Rozměry jsou: kratší odvěsna 6cm, delší odvěsna 8cm.
Tenká destička tvaru pravoúhlého trojúhelníku se jednou otočí kolem kratší odvěsny a podruhé kolem delší odvěsny. Rotací se popíší kužely. Mají stejný objem? Rozměry jsou: kratší odvěsna 6cm, delší odvěsna 8cm. - Faktor měřítka
 Kostka má povrch 64 stop². Henrieta vytvoří zmenšení této kostky pomocí koeficientu měřítka 0,5. Jaký je povrch zmenšené kostky?
Kostka má povrch 64 stop². Henrieta vytvoří zmenšení této kostky pomocí koeficientu měřítka 0,5. Jaký je povrch zmenšené kostky? - Rovnostranné těleso
 Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa.
Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa. - 3B hranol - stan
 Kolik m² látky je třeba na zhotovení stanu pravidelného 3-bokého hranolu pokud je třeba počítat s 2% rezervou látky? Rozměry - 2m 1,6m a výška 1,4m
Kolik m² látky je třeba na zhotovení stanu pravidelného 3-bokého hranolu pokud je třeba počítat s 2% rezervou látky? Rozměry - 2m 1,6m a výška 1,4m - Povrch rotačního válce
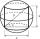 Obsah pláště rotačního válce je polovina obsahu jeho povrchu. Vypočítejte povrch válce, když víte, že úhlopříčka osového řezu je 5cm.
Obsah pláště rotačního válce je polovina obsahu jeho povrchu. Vypočítejte povrch válce, když víte, že úhlopříčka osového řezu je 5cm. - Poměr rychlosti
 Určete, v jakém poměru jsou rychlosti kapaliny v různých částech potrubí (jedna část má průměr 5 cm a druhá má průměr 3 cm), když víte, že v každém místě kapaliny je součin plochy průzeřu trubice [S] a rychlosti kapaliny [v] stejný.
Určete, v jakém poměru jsou rychlosti kapaliny v různých částech potrubí (jedna část má průměr 5 cm a druhá má průměr 3 cm), když víte, že v každém místě kapaliny je součin plochy průzeřu trubice [S] a rychlosti kapaliny [v] stejný. - Přesýpací hodiny
 Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek
Přesýpací hodiny sestávají ze dvou shodných nádobek ve tvaru rotačních kuželů. Pro jednoduchost předpokládáme, že koužely se dotýkají pouze svými vrcholy. Písek sahá do poloviny výšky spodního kužele. Po překlopení hodí trvá přesně 21 minut, než se písek - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
