Základní operace a pojmy - slovní úlohy a příklady - strana 284 z 303
Počet nalezených příkladů: 6060
- Světlo
 Světlo prochází rozhraním mezi vzduchem a sklem s indexem lomu 1,5. Určete: a) úhel lomu, dopadá-li světlo na rozhraní ze vzduchu pod úhlem 40°. b) úhel lomu, dopadá-li světlo na rozhraní ze skla pod úhlem 40°. c) úhel dopadu, jestliže se světlo při dopad
Světlo prochází rozhraním mezi vzduchem a sklem s indexem lomu 1,5. Určete: a) úhel lomu, dopadá-li světlo na rozhraní ze vzduchu pod úhlem 40°. b) úhel lomu, dopadá-li světlo na rozhraní ze skla pod úhlem 40°. c) úhel dopadu, jestliže se světlo při dopad - Pravděpodobnost vyklíčení rostlin
 pravděpodobnost, ze ze semínka vyroste rostlina je 75%. Jaká je pravděpodobnost, že když sestavíme 6 semínek vyroste 5 rostlin.
pravděpodobnost, ze ze semínka vyroste rostlina je 75%. Jaká je pravděpodobnost, že když sestavíme 6 semínek vyroste 5 rostlin. - Vzdálenosti - majáky
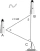 Dva majáky A, B spatřily loď, jak je znázorněno na obrázku. Jaká je vzdálenost mezi lodí a majákem A s přesností na jednu desetinu námořní míle? Obrázek - vzdálenost mezi majáky A a B je 40 námořních mil. Z bodu A je vidět úhel pohledu 57° a z bodu B pod
Dva majáky A, B spatřily loď, jak je znázorněno na obrázku. Jaká je vzdálenost mezi lodí a majákem A s přesností na jednu desetinu námořní míle? Obrázek - vzdálenost mezi majáky A a B je 40 námořních mil. Z bodu A je vidět úhel pohledu 57° a z bodu B pod - Uspořádání knih
 Knihkupectví Levný Jožko snižuje ceny knih o matematice k propagaci. Obchod má 6 knih o algebře, 6 knih o geometrii a 5 knih o statistice, které lze uspořádat na polici. Knihy stejného druhu se umístí vedle sebe. Kolika způsoby mohou být tyto knihy uspořá
Knihkupectví Levný Jožko snižuje ceny knih o matematice k propagaci. Obchod má 6 knih o algebře, 6 knih o geometrii a 5 knih o statistice, které lze uspořádat na polici. Knihy stejného druhu se umístí vedle sebe. Kolika způsoby mohou být tyto knihy uspořá - Pravděpodobnost hodu kostkou
 Pravděpodobnost, že při 3 hodech kostkou padne 6 právě jednou je?
Pravděpodobnost, že při 3 hodech kostkou padne 6 právě jednou je? - V jedné třetině
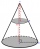 Objem pravého kruhového kužele je 5 litrů. Vypočítejte objem dvou částí, na které je kužel rozdělen rovinou rovnoběžnou se základnou, v jedné třetině vzdálenosti od vrcholu k základně.
Objem pravého kruhového kužele je 5 litrů. Vypočítejte objem dvou částí, na které je kužel rozdělen rovinou rovnoběžnou se základnou, v jedné třetině vzdálenosti od vrcholu k základně. - Tři ženy
 Uvádí se, že 72% pracujících žen používá počítače v práci. Vyberte si 3 ženy náhodně, zjistěte pravděpodobnost, že všechny 3 ženy budou při práci používat počítač.
Uvádí se, že 72% pracujících žen používá počítače v práci. Vyberte si 3 ženy náhodně, zjistěte pravděpodobnost, že všechny 3 ženy budou při práci používat počítač. - Porucha TV
 Televizor má za 10000 hodín v průměru 20 poruch. Určete pravděpodobnost poruchy televizoru za 700 hodin provozu.
Televizor má za 10000 hodín v průměru 20 poruch. Určete pravděpodobnost poruchy televizoru za 700 hodin provozu. - Koule ve kuželi
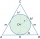 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t - Pravděpodobnost na mřížce
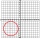 Pravoúhlá mřížka se skládá ze dvou navzájem kolmých soustav rovnoběžných přímek s rozestupem 2. Na tuto rovinu hodíme kruh o průměru 1. Vypočítejte pravděpodobnost, že tento kruh: a) překryje některou z přímek; b) překryje některý z průsečíků přímek?
Pravoúhlá mřížka se skládá ze dvou navzájem kolmých soustav rovnoběžných přímek s rozestupem 2. Na tuto rovinu hodíme kruh o průměru 1. Vypočítejte pravděpodobnost, že tento kruh: a) překryje některou z přímek; b) překryje některý z průsečíků přímek? - Přímky
 V kolika bodech se protne 15 různých přímek, pokud žádné dvě nejsou rovnoběžné?
V kolika bodech se protne 15 různých přímek, pokud žádné dvě nejsou rovnoběžné? - Výškový rozdíl
 Jaký výškový rozdíl překonáme, pokud přejdeme cestu dlouhou 1 km se stoupáním 21 promile?
Jaký výškový rozdíl překonáme, pokud přejdeme cestu dlouhou 1 km se stoupáním 21 promile? - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Bod na úsečce
 Najděte bod P na úsečce AB tak, že |AP| = r |AB| . Souřadnice koncových bodů: A = (−2, 0, 1), B = (10, 8, 5), poměr r = 1/4.
Najděte bod P na úsečce AB tak, že |AP| = r |AB| . Souřadnice koncových bodů: A = (−2, 0, 1), B = (10, 8, 5), poměr r = 1/4. - Na vrcholu
 Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou?
Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou? - Test s výběrem odpovědí
 Test má 10 otázek s výběrem odpovědí. Na výběr správné odpovědi jsou čtyři možnosti A, B, C, D, přičemž správná je vždy jedna z nich. Kolik je všech různých možností pro odpovědi v tomto testu, a) odpoví-li jeho řešitel na každou otázku b) odpoví-li na ka
Test má 10 otázek s výběrem odpovědí. Na výběr správné odpovědi jsou čtyři možnosti A, B, C, D, přičemž správná je vždy jedna z nich. Kolik je všech různých možností pro odpovědi v tomto testu, a) odpoví-li jeho řešitel na každou otázku b) odpoví-li na ka - V terénu - věta SSU
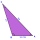 V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele.
V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele. - Vzdálenost cíle
 Cíl C pozorovali ze dvou dělostřeleckých pozorovatelen A, B, které jsou od sebe vzdáleny 975m, přitom velikost úhlu BAC je 63°, velikost ABC je 48°. Vypočítejte vzdálenost bodů A a C.
Cíl C pozorovali ze dvou dělostřeleckých pozorovatelen A, B, které jsou od sebe vzdáleny 975m, přitom velikost úhlu BAC je 63°, velikost ABC je 48°. Vypočítejte vzdálenost bodů A a C. - Spotřeba plechu
 Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,3m. Odchylka strany od roviny podstavy je 36°. Vypočítejte spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad.
Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,3m. Odchylka strany od roviny podstavy je 36°. Vypočítejte spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad. - Nepřístupna místa
 Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji.
Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
