Tetiva
Na kružnici k (S; r = 8 cm) sú rôzne body A, B spojené úsečkou/AB/ = 12 cm. Stred AB označ S'. Vypočítajte/SS'/. Vykonaj náčrtok.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Narysuj 4
Narýsuj úsečku KL=55 mm. Narýsuj kružnicu k so stredom K a polomerom 4 cm. Vyznačuj body tak, aby patrili kružnici a spájaj ich s bodom L. - Štvorec ABCD
Zostrojte štvorec ABCD so stredom S [3,2] a stranou a = 4 cm. Vrchol A leží na osi x. Zostrojte jeho obraz v posunutí danom orientovanou úsečkou SS'; S` [-1, - 4]. - Stred kružnice
Je daná ľubovolná kružnica k, ktorá nemá vyznačený stred. Pomocou vhodnej konštrukcie nájdi stred kružnice k. Vyskúšaj na 2 rôznych kružniciach. - Tetiva 2
Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k. - Vektory - základné operácie
Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určte súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určte súradnice vektora w=-2.u - V kružnici 3
V kružnici k s polomerom 13 cm je tetiva AB. Stred C tetivy AB je od stredu S kruž nice vzdialený 5 cm. Aká dlhá je tetiva AB? - Na kružnici
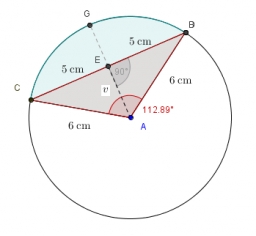
Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC.
