Šesťuholník nepravidelný
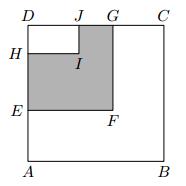
Na obrázku je štvorec ABCD, štvorec EFGD a obdĺžnik HIJD. Body J a G ležia na strane CD, pričom platí |DJ| < |DG| a body H a E ležia na strane DA, pričom platí /DH/ < /DE/. Ďalej vieme, že/DJ/ = /GC/. Šesťuholník ABCGFE má obvod 96 cm, šesťuholník EFGJIH má obvod 60 cm a obdĺžnik HIJD má obvod 28 cm. Určte obsah šesťuholníka EFGJIH.
Správna odpoveď:
Zobrazujem 1 komentár:
Mo-radce
Nápoveda. Dokážete určiť dĺžku niektoré úsečky, bez toho aby ste k tomu použili viac ako jeden zadaný rozmer?
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
Riešenie.
Zistíme rozmery štvorca EFGD a obdĺžnika HIJD, aby sme stanovili ich obsahy. Rozdiel týchto obsahov predstavuje žiadaný obsah šesťuholníka EFGJIH. Zadaný obvod šesťuholníka EFGJIH je rovný obvodu štvorca EFGD, lebo |JU| = |DH| a |HI| = |DJ|. Strana GD má teda veľkosť 60:4 = 15 (cm). Podobne zadaný obvod šesťuholníka ABCGFE je rovný obvodu štvorca ABCD, veľkosť strany CD je teda 96:4 = 24 (cm). Rozdiel dĺžok strán týchto dvoch štvorcov je rovný dĺžke úsečky GC, ktorá je podľa zadania rovná dĺžke úsečky DJ:
|DJ| = |GC| = 24 - 15 = 9 (cm).
Pomocou známeho obvodu obdĺžnika HIJD a dĺžky strany DJ stanovíme aj druhý rozmer tohto obdĺžnika:
|JI| = (28 - 2 · 9): 2 = 5 (cm).
Teraz máme všetky údaje potrebné na stanovenie obsahov štvorca EF GD a obdĺžnika HIJD:
S (EFGD) = 15 · 15 = 225 cm2
S (HIJD) = 9 · 5 = 45 cm2
Hľadaný obsah šesťuholníka teda je S (EFGJIH) = 225 - 45 = 180 cm2.
8 rokov 1 Like
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Zastroj
 Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie.
Zastroj rovnoramenný trojuholník ABY zo základňou AB dĺžky 5 cm a uhlom pri hlavnom vrchole veľkosti 50°. Zapíše postup konštrukcie. - Dve tetivy
 Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami.
Dané sú dve úsečky rôznych dĺžok. Zostrojte kružnicu k tak, aby obe úsečky boli jej tetivami. - Dve družnice
 Zostroj 2 kružnice tak aby ich stredy boli od seba vzdialene 5 cm a: a-nemali spoločný dotyk b- mali spoločný bod c-mali 2 spoločné body
Zostroj 2 kružnice tak aby ich stredy boli od seba vzdialene 5 cm a: a-nemali spoločný dotyk b- mali spoločný bod c-mali 2 spoločné body - RST trojuholník
 Zisti, či je možné zostrojiť daný trojuholník a podľa, ktorej vety : RS = 2,5 cm ST = 7 cm TR = 4,5 cm
Zisti, či je možné zostrojiť daný trojuholník a podľa, ktorej vety : RS = 2,5 cm ST = 7 cm TR = 4,5 cm
- Zostroj 22
 Zostroj kosoštvorec, ktorý ma dĺžku strany 5 cm a výšku 4,5 cm. Náčrt: Rozbor: Konštrukcia: Postup:
Zostroj kosoštvorec, ktorý ma dĺžku strany 5 cm a výšku 4,5 cm. Náčrt: Rozbor: Konštrukcia: Postup: - Vo všeobecnom
 Vo všeobecnom lichobežníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; |
Vo všeobecnom lichobežníku VLAK platí: |VL| = 5,5cm; |VK| = 3,5cm; |LK| = 4,8cm; | - Priesečník uhlopriečok
 Zostroj rovnobežník ABCD, ak a=5 cm, Výška na stranu a je 5 cm a uhol ASB = 120 stupňov. S je priesečník uhlopriečok.
Zostroj rovnobežník ABCD, ak a=5 cm, Výška na stranu a je 5 cm a uhol ASB = 120 stupňov. S je priesečník uhlopriečok. - Zostroj 21
 Zostroj obdĺžnik ABCD ak a=8cm a dĺžka uhlopriečky AC je 13cm. Odmeraj dĺžku strán obdĺžnika.
Zostroj obdĺžnik ABCD ak a=8cm a dĺžka uhlopriečky AC je 13cm. Odmeraj dĺžku strán obdĺžnika. - Ostrouhlý trojuholník
 Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC.
Daný je ostrouhlý trojuholník ABC. Na polpriamkach opačných k BA a CA ležia postupne body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokážte, že stred kružnice opísanej trojuholníku ADE leží na kružnici opísanej trojuholníku ABC.
- Uhlopriečka 36
 Narysuj štvorec EFIJ, ak EI sa rovná 7cm.
Narysuj štvorec EFIJ, ak EI sa rovná 7cm. - Ťažnica a výška
 Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm
Zostroj trojuholník KLM ak strana m=6,5cm, ťažnica tm=4cm, výška na stranu m: vm=3,2cm - Strana výška a uhol
 Daná je úsečka BC dĺžky 6cm. Zostroj trojuholník tak, aby uhol BAC mal veľkosť 50°a výška na stranu a mala 5,5 cm. Ďakujem pekne.
Daná je úsečka BC dĺžky 6cm. Zostroj trojuholník tak, aby uhol BAC mal veľkosť 50°a výška na stranu a mala 5,5 cm. Ďakujem pekne. - Načrtnite 2
 Načrtnite sieť štvorbokého hranola, ktorého podstavou je obdĺžnik 1 cm x 3 cm a vysoký je 5 cm.
Načrtnite sieť štvorbokého hranola, ktorého podstavou je obdĺžnik 1 cm x 3 cm a vysoký je 5 cm. - ABCD(AB//CD): 70454
 Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60°
Zostrojte lichobežník ABCD(AB//CD): |AB|=7cm |BC|=3,5cm |CD|=4cm A veľkosť uhla ABC=60°
- Zostroj 20
 Zostroj trojuholník HOP, ak o=6 cm, h=8cm a |PHO|=90°
Zostroj trojuholník HOP, ak o=6 cm, h=8cm a |PHO|=90° - Stredovo súmerný
 Koľko štvorčekov v sieti na obrázku treba ešte vymalovať, aby bol stredovo súmerný? štvorček - x x; o; o; x o; o; x; o x; o; o; o o; x; o; o toto je nakres štvorčekovej siete, kde vyfarbené štvorce sú x. Dakujem Lucia
Koľko štvorčekov v sieti na obrázku treba ešte vymalovať, aby bol stredovo súmerný? štvorček - x x; o; o; x o; o; x; o x; o; o; o o; x; o; o toto je nakres štvorčekovej siete, kde vyfarbené štvorce sú x. Dakujem Lucia - Zostrojte 11
 Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov
