Spoločná tetiva
Spoločná tetiva dvoch kružníc k1 a k2 má dĺžku 3,8 cm. Táto tetiva zviera s polomerom r1 kružnice k1 uhol o veľkosti 47° a s polomerom r2 kružnice k2 uhol 24° 30 '. Vypočítajte oba polomery a vzdialenosť oboch stredov kružníc.
Správna odpoveď:
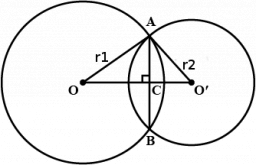
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- planimetria
- pravouhlý trojuholník
- trojuholník
- tetiva
- goniometria a trigonometria
- sínus
- kosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Dve kružnice 2
Dve kružnice s rovnykými polomermi 58 mm sa pretínajú v dvoch bodoch. Ich spoločná tetiva je dlhá 80 mm. Aká je vzdialenosť stredov týchto kružníc? - Spoločná tetiva
Dve kružnice s polomermi 16 cm a 10 cm sa pretínajú v dvoch bodoch. Ich spoločná tetiva je dlhá 12 cm. Aká je vzdialenosť stredov týchto kružníc? - Tetiva 2
Bod A má od stredu kružnice s polomerom r = 5 cm vzdialenosť 13 cm. Vypočítajte dĺžku tetivy spájajúca body dotyku T1 a T2 dotyčníc vedených z bodu A ku kružnici k. - Tetiva
Akú dĺžku má tetiva AB, ktorej vzdialenosť od stredu S kružnice k(S, 92 cm) sa rovná 10 cm?
- Štvorec a kružnice
Štvorcu o strane 80 mm je opísaná a vpísaná kružnica. Určite polomery oboch kružnic. - Vedľajšieho 72874
V kruhu s polomerom 6 cm je struna nakreslená 3 cm od stredu. Vypočítajte uhol, ktorý zviera kord v strede kruhu Nájdite teda dĺžku vedľajšieho oblúka odrezaného akordom. - Telesová 4
Telesová uhlopriečka pravidelného štvorbokého hranola zviera s podstavou uhol veľkosti 60°. Hrana podstavy má dĺžku 10cm. Vypočítajte objem telesa.
