Rast populácie
Koľko ľudí bude na zemi z dvoch ľudí za 5000 rokov, ak sa narodia každému páru vždy vo veku 25-35 rokov 4 deti, 2x chlapec a 2x dievča a každý človek sa dožije 75rokov?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- geometrická postupnosť
- nekonečný geometrický rad
- vyjadrenie neznámej zo vzorca
- základné funkcie
- úvaha
- exponenciála
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Určte 17
 Určte s5 geometrickej postupnosti, ak platí: a1 + a2 = 10 a a4 - a2 = 120
Určte s5 geometrickej postupnosti, ak platí: a1 + a2 = 10 a a4 - a2 = 120 - Cvičenci 3
 Cvičenci stoja na značkách v radoch vzdialených od seba presne 1,5 m. Tvoria rozširujúci sa trojuholníkový klin (v každom nasledujúcom rade je o jedného cvičenca viac), pričom vzdialenosť čelného cvičenca od zadného radu je 30 m. Určte počet cvičencov.
Cvičenci stoja na značkách v radoch vzdialených od seba presne 1,5 m. Tvoria rozširujúci sa trojuholníkový klin (v každom nasledujúcom rade je o jedného cvičenca viac), pričom vzdialenosť čelného cvičenca od zadného radu je 30 m. Určte počet cvičencov. - Kvety
 Každý deň sa z kvetu rozvinú dva nové kvety a každý z týchto nových kvetov nesie každý deň dva kvety. Koľko kvetov je už rozkvitnutých v záhrade po ôsmich dňoch?
Každý deň sa z kvetu rozvinú dva nové kvety a každý z týchto nových kvetov nesie každý deň dva kvety. Koľko kvetov je už rozkvitnutých v záhrade po ôsmich dňoch? - Hypotéka - súčasná hodnota
 Banka požičia rodine 90 000 dolárov pri ročnej úrokovej sadzbe 4,5% na kúpu domu. Rodina súhlasí so splácaním pôžičky formou mesačných splátok počas obdobia 15 rokov. Koľko by mala byť mesačná splátka, aby sa dlh splatil za 15 rokov?
Banka požičia rodine 90 000 dolárov pri ročnej úrokovej sadzbe 4,5% na kúpu domu. Rodina súhlasí so splácaním pôžičky formou mesačných splátok počas obdobia 15 rokov. Koľko by mala byť mesačná splátka, aby sa dlh splatil za 15 rokov?
- Nájdite 8
 Nájdite zvyšok po delení, keď delíme súčet 1!+2!+3!+. .. . . +300! číslom 13.
Nájdite zvyšok po delení, keď delíme súčet 1!+2!+3!+. .. . . +300! číslom 13. - Súčet GP
 Určte súčet GP 30, 6, 1,2, len prvých 5 členov. Aký je súčet všetkých členov (do nekonečna)?
Určte súčet GP 30, 6, 1,2, len prvých 5 členov. Aký je súčet všetkých členov (do nekonečna)? - Exponenciálny pokles
 Nádrž obsahuje 55 litrov vody. Voda tečie rýchlosťou 7% za minútu. Ako dlho trvá vypustenie nádrže?
Nádrž obsahuje 55 litrov vody. Voda tečie rýchlosťou 7% za minútu. Ako dlho trvá vypustenie nádrže? - Cirkus
 Príchod cirkusu do Plzne zaznamenal ráno o 08:00 jeden občan mesta a túto informáciu odovzdal 08:15 ďalším trom obyvateľom mesta. Každý z týchto troch ľudí potom o 08:30 informoval ďalších troch obyvateľov, títo potom opäť v 08:45 odovzdali zvesť o prícho
Príchod cirkusu do Plzne zaznamenal ráno o 08:00 jeden občan mesta a túto informáciu odovzdal 08:15 ďalším trom obyvateľom mesta. Každý z týchto troch ľudí potom o 08:30 informoval ďalších troch obyvateľov, títo potom opäť v 08:45 odovzdali zvesť o prícho - Súčet obsahov
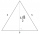 Nád výškou rovnostranného trojuholníka ABC je zostrojený rovnostranný trojuholník A1, B1, C1, nad jeho výškou je zostrojený rovnostranný trojuholník A2, B2, C2, atd. Sa postup neustale opakuje. Aký je veľký súčet obsahov všetkých trojuholníkov, ak strana
Nád výškou rovnostranného trojuholníka ABC je zostrojený rovnostranný trojuholník A1, B1, C1, nad jeho výškou je zostrojený rovnostranný trojuholník A2, B2, C2, atd. Sa postup neustale opakuje. Aký je veľký súčet obsahov všetkých trojuholníkov, ak strana
- Rovnicu: 6738
 V množine N riešte danú rovnicu: 1 – x + x² – x³ + x4 – x5 + …. + = 1/3
V množine N riešte danú rovnicu: 1 – x + x² – x³ + x4 – x5 + …. + = 1/3 - Črievička
 Črievička (jednobunkový organizmus) za ideálnych podmienok sa rozdelí na 2 črievičky v priemere každých 27 hodín, Keby všetky črievičky zostáva na žive, koľko by ich bolo za 7 dní?
Črievička (jednobunkový organizmus) za ideálnych podmienok sa rozdelí na 2 črievičky v priemere každých 27 hodín, Keby všetky črievičky zostáva na žive, koľko by ich bolo za 7 dní? - Rad, rady ...
 Určte súčet nekonečného radu: 1/3+1/9+1/27+1/81.. .
Určte súčet nekonečného radu: 1/3+1/9+1/27+1/81.. . - Nekonečný des. rozvoj
 Predstav si nekonečné, desatinné číslo 0,99999999 .. ... ... ... čiže desatinnú čiarku a za ňou nekonečnú postupnosť deviatok. Urči o koľko je toto číslo menšie ako číslo 1. Za vyriešenie tohto náročného príkladu vopred ďakujem.
Predstav si nekonečné, desatinné číslo 0,99999999 .. ... ... ... čiže desatinnú čiarku a za ňou nekonečnú postupnosť deviatok. Urči o koľko je toto číslo menšie ako číslo 1. Za vyriešenie tohto náročného príkladu vopred ďakujem. - Do kina
 Janka sa v 8 hod dozvedela, že všetkých 1093 žiakov školy pôjde do kina. Počas 20 min. to povedala 3 kamarátom. Každý z nich to opäť za 20 min. povedal ďalším trom. Týmto spôsobom sa správa šírila ďalej. V koľko hodín sa ju dozvedeli všetky deti v škole?
Janka sa v 8 hod dozvedela, že všetkých 1093 žiakov školy pôjde do kina. Počas 20 min. to povedala 3 kamarátom. Každý z nich to opäť za 20 min. povedal ďalším trom. Týmto spôsobom sa správa šírila ďalej. V koľko hodín sa ju dozvedeli všetky deti v škole?
- Zázračný strom
 Zázračný strom rastie tak rýchlo, že sa prvý deň zväčší jeho výška o polovicu celkovej výšky, druhý deň o tretinu, tretí deň o štvrtinu, atď. Koľkokrát sa zväčší jeho výška za 3 dní?
Zázračný strom rastie tak rýchlo, že sa prvý deň zväčší jeho výška o polovicu celkovej výšky, druhý deň o tretinu, tretí deň o štvrtinu, atď. Koľkokrát sa zväčší jeho výška za 3 dní? - Hod kockami
 Keď hádžeš desiatimi kockami naraz, tak v priemere hodíš 35. Koľko priemerne hodíš, ak vždy keď padne šestka hádžeš tou kockou znova?
Keď hádžeš desiatimi kockami naraz, tak v priemere hodíš 35. Koľko priemerne hodíš, ak vždy keď padne šestka hádžeš tou kockou znova? - Babka k babce
 Prvý deň si odložím 1 cent a každý ďaľší o cent viac. Koľko si nasporim za rok (365 dní)?
Prvý deň si odložím 1 cent a každý ďaľší o cent viac. Koľko si nasporim za rok (365 dní)?
