Vypočítajte 229
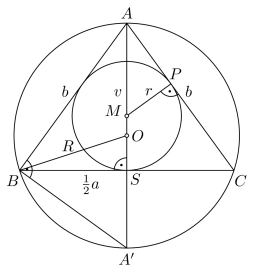
Vypočítajte obsah kruhu, do ktorého je vyrezaný otvor v tvare rovnostranného trojuholníka, keď priemer kruhu, d=32 mm a strana trojuholníka a=20,8 mm
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikaplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Strana trojuholníka
Mam kruh s priemerom 6,4 cm. Potrebujem zistiť dĺžku strany rovnostranného trojuholníka vpísaného do kruhu. - Štvorček
Zo štvorca o obvode 12 dm je vyrezaný štvorček, ktorého strana je tretinou strany štvorca. Aký je obsah zvyšné časti? - Vypočítajte
Vypočítajte dĺžku strany rovnostranného trojuholníka, ktorého obsah je 50 cm štvorcových. - Stĺp
Vypočítajte objem a povrch podporného stĺpu tvare kolmého štvorbokého hranola, ktorého podstavou je kosoštvorec s uhlopriečku u1 = 102 cm, u2 = 64 cm. Výška stĺpa je 1,5 m. - Obsah trojuholníka
Pole má tvar rovnostranného trojuholníka. Vypočítaj jeho obsah, keď vieš, že strana je dlhá 280 metrov. - Trojuholníka PT-20
Do kruhu s priemerom 20 cm bol vpísaný pravouhlý trojuholník, ktorého prepona je priemerom kruhu má čo najväčší obsah. Vypočítaj obsah tohto trojuholníka. - Rovnostranný trojuholník Vypočítajte obsah rovnostranného trojuholníka, ktorého obvod je 72 cm.
