MO B 2019 - uloha 2
Prirodzené číslo n má aspoň 73 dvojciferných deliteľov. Dokážte, že jedným z nich je číslo 60. Uveďte tiež príklad čísla n, ktoré má práve 73 dvojciferných deliteľov, vrátane náležitého zdôvodnenia.
Správna odpoveď:

Zobrazujem 6 komentárov:
Dr Math
takto, 60 = 4*3*5
vypisem si dvojciferne cisla ktore nie su delitelne 5. Je ich 72. Podozrive cislo. V mnozine tychto 72 cisel su zarucene cisla ktore su delitelne cislom 3 aj 4 (napr. cislo 36 ...). Teda ak k tymto 72 cislam pridam akekolvek dvojciferne cislo, je zarucene delitelne 5 (lebo som vynechal len delitelne piatimi). Ak by som vynasobil vsetkych 73 cisel, zarucene mam ze vysledok nasobenia bude delitelny 3,4 aj 5, a preto aj 60.
vypisem si dvojciferne cisla ktore nie su delitelne 5. Je ich 72. Podozrive cislo. V mnozine tychto 72 cisel su zarucene cisla ktore su delitelne cislom 3 aj 4 (napr. cislo 36 ...). Teda ak k tymto 72 cislam pridam akekolvek dvojciferne cislo, je zarucene delitelne 5 (lebo som vynechal len delitelne piatimi). Ak by som vynasobil vsetkych 73 cisel, zarucene mam ze vysledok nasobenia bude delitelny 3,4 aj 5, a preto aj 60.
Dr Math
tych 72 zistim tak ze mame 100-10 = 90 ruznych dvojcifernych cisel. dvojcifernych cisel delitelnych 5 je 100/5 - 2 = 18. 90-18=72
Dr Math
cislo s presne 73 delitelmi najdem tak ze vynasobim prvych 73 prvocisel.,,, ak toto neviete, MO radsej nerieste... Samozrejme da sa to aj inak, napr. ked je v prvociselnom rozklade zlozene cislo 4 = 22, tak to zdvojnasobuje pocet vsetkych delitelov... To je potom komplikovanejsie.
Žiak
Zle som sa vyjadril. Práve 73 dvojciferných deliteľov - Podľa zadania. (Prvých 73 hocijakých je jasné, že prvočísla znásobiť.)
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Nekoneční desetinný rozvoj
 Určite, ktorá číslica je na 1000. mieste za desatinnou čiarkou v desatinnom rozvoji čísla - zlomku 9/28.
Určite, ktorá číslica je na 1000. mieste za desatinnou čiarkou v desatinnom rozvoji čísla - zlomku 9/28. - Keby hodiny
 Keby hodiny ukazovali o štvrťhodinu viac, bolo by na nich o 10minút 10 hodín. Koľko hodín ukazujú?
Keby hodiny ukazovali o štvrťhodinu viac, bolo by na nich o 10minút 10 hodín. Koľko hodín ukazujú? - Nájdite 8
 Nájdite zvyšok po delení, keď delíme súčet 1!+2!+3!+. .. . . +300! číslom 13.
Nájdite zvyšok po delení, keď delíme súčet 1!+2!+3!+. .. . . +300! číslom 13. - Predvčerom 13711
 Ak bola predvčerom nedeľa aký deň v týždni bude oddnes za 50 dní. (0 = pondelok, 6 = nedeľa)
Ak bola predvčerom nedeľa aký deň v týždni bude oddnes za 50 dní. (0 = pondelok, 6 = nedeľa)
- Z5–I–4 MO 2019
 Vojto začal vypisovať do zošita číslo terajšieho školského roku 2019202020192020. . . A tak pokračoval stále ďalej. Keď napísal 2020 cifier, prestalo ho to baviť. Koľko tak napísal dvojok?
Vojto začal vypisovať do zošita číslo terajšieho školského roku 2019202020192020. . . A tak pokračoval stále ďalej. Keď napísal 2020 cifier, prestalo ho to baviť. Koľko tak napísal dvojok? - Reštaurácia
 U neskrotného diviaka mali pred bitkou tridsať stolov označených prirodzenými číslami 2 až 31. Práve dva stoly patrili do salónika. Aby personál pri inventúre zistil, ktoré dva to sú, používal trik. Na dverách salónika bola tabuľka s číslom, ktoré nebolo
U neskrotného diviaka mali pred bitkou tridsať stolov označených prirodzenými číslami 2 až 31. Práve dva stoly patrili do salónika. Aby personál pri inventúre zistil, ktoré dva to sú, používal trik. Na dverách salónika bola tabuľka s číslom, ktoré nebolo - MO Z6–I–3 2018
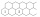 Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude
Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude - Prsty
 Janka počíta na jednej ruke po jednom. Začína počítať od palca cez ukazovák, prostredník a prstenník, príde k malíčku a má číslo 5. Potom sa hned vracia k prstenníku (6), na prostredník (7), ukazovák (8), palec (9) a zase na ukazovák (10), prostredník (11
Janka počíta na jednej ruke po jednom. Začína počítať od palca cez ukazovák, prostredník a prstenník, príde k malíčku a má číslo 5. Potom sa hned vracia k prstenníku (6), na prostredník (7), ukazovák (8), palec (9) a zase na ukazovák (10), prostredník (11 - Elektrina
 V utorok o 6 hodine bola prerušená dodávka elektriny na 156 h. Ktorý deň (1=pondeli, ... 7 =nedeľa) av koľko hodín bola dodávka elektriny obnovená?
V utorok o 6 hodine bola prerušená dodávka elektriny na 156 h. Ktorý deň (1=pondeli, ... 7 =nedeľa) av koľko hodín bola dodávka elektriny obnovená?
- Zvyšok po delení
 Aký zvyšok dá pri delení číslom 9 číslo 10 na 47 - 111?
Aký zvyšok dá pri delení číslom 9 číslo 10 na 47 - 111? - Vianoce
 Otec povedal. ,, Presne o 56 hodín si sadneme k štedrovečernému stolu. " Koľkého bolo a koľko bolo hodín keď otecko povedal túto vetu? K štedrovečernému stolu u nich sadajú presne o 18-tej hodine.
Otec povedal. ,, Presne o 56 hodín si sadneme k štedrovečernému stolu. " Koľkého bolo a koľko bolo hodín keď otecko povedal túto vetu? K štedrovečernému stolu u nich sadajú presne o 18-tej hodine. - Zvonkohra MO - Z5 - 1 - 66
 Zvonkohra na nádvorí hrá o každej celej hodine krátku skladbu, a to počínajúc 8. a končiac 22. hodinou. Skladieb je celkom osemnásť, o celej hodine sa hrá vždy iba jedna a po odohraní všetkých osemnástich sa začína v rovnakom poradí znova. Oľga a Ľuboš bo
Zvonkohra na nádvorí hrá o každej celej hodine krátku skladbu, a to počínajúc 8. a končiac 22. hodinou. Skladieb je celkom osemnásť, o celej hodine sa hrá vždy iba jedna a po odohraní všetkých osemnástich sa začína v rovnakom poradí znova. Oľga a Ľuboš bo - Bača a ovce
 Bača má menej ako 500 oviec , ak ich zoradí do 4 radu ostanú mu 3 ovce , ak ich zoradí do 5 radu , ostanú mu 4 ovce a keď ich zoradí do 6 radu , ostane mu 5 oviec. Ale môže ich zoradiť presne do 7 radu.
Bača má menej ako 500 oviec , ak ich zoradí do 4 radu ostanú mu 3 ovce , ak ich zoradí do 5 radu , ostanú mu 4 ovce a keď ich zoradí do 6 radu , ostane mu 5 oviec. Ale môže ich zoradiť presne do 7 radu. - Babkine hodiny
 Babkine hodiny sa každú hodinu omeškajú o pol minúty. Babka ich o 8,00 hod. nastaví presne. Koľko budú hodiny ukazovať o 24 hod.?
Babkine hodiny sa každú hodinu omeškajú o pol minúty. Babka ich o 8,00 hod. nastaví presne. Koľko budú hodiny ukazovať o 24 hod.?
- Ručičky na hodinách
 Ručičky na hodinách ukazujú čas 12 hodín a 2 minúty. Vypočítaj veľkosť ostrého uhla, ktorý budú zvierať o 3 hodiny neskôr.
Ručičky na hodinách ukazujú čas 12 hodín a 2 minúty. Vypočítaj veľkosť ostrého uhla, ktorý budú zvierať o 3 hodiny neskôr. - Vianoce
 Presne o 76 hodín si sadneme k štedrovečernému stolu. Koľkého bolo a koľko bolo hodín keď otecko povedal túto vetu. K štedrovečernému stolu u nich sadajú presne o 18-tej hodine.
Presne o 76 hodín si sadneme k štedrovečernému stolu. Koľkého bolo a koľko bolo hodín keď otecko povedal túto vetu. K štedrovečernému stolu u nich sadajú presne o 18-tej hodine. - Zvyšky
 Daná je množina čísel { 170; 244; 299; 333; 351; 391; 423; 644 }. Deľte tieto čísla číslom 66. Určite množinu zvyškou a ako výsledok udajte súčet týchto zvyškov.
Daná je množina čísel { 170; 244; 299; 333; 351; 391; 423; 644 }. Deľte tieto čísla číslom 66. Určite množinu zvyškou a ako výsledok udajte súčet týchto zvyškov.
