Vzdálenost mezi body
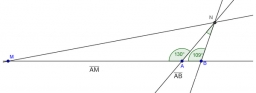
Určete vzdálenost dvou míst M, N, mezi kterými je překážka, takže místo N z místa M není viditelné. Byly měřeny úhly MAN = 130°, NBM = 109° a vzdálenosti |AM| = 54, |BM| = 60, přičemž body A, B, M leží na jedné přímce.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Nepřístupne místa
Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině. - Nepřístupna místa
Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji. - Stejná teplota
Teploty dvou míst byly měřeny současně. Teplota ve městě A byla 60 stupňů °F a stoupala konstantní rychlostí 2 stupně za hodinu. Teplota ve městě B byla 40°F a stoupala konstantní rychlostí 10°F za hodinu Najděte čas v hodinách, kdy je teplota v obou měst - Obsah Č.T.
Je dán čtverec EQBO, přičemž |QB|=24. Vypočítejte obsah trojúhelníku EOA, kde vrchol A leží na přímce BQ. - Triangulace - výškové úhly
Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž? - Strom 14
Mezi body A, B je 50m. Z místa A, vidíme strom pod ůhlem 18°. Z místa B, vidíme strom 3x velkým ůhlem. Jak vysoký je strom? - Souřadnice bodu B
V trojúhelníku ABC určete souřadnice bodu B, pokud víte, že body A, B leží na přímce 3x-y-5=0, body A, C leží na přímce 2x+3y+4=0, bod C leží na souřadnicové ose x a úhel u vrcholu C je pravý.
