Prekážka
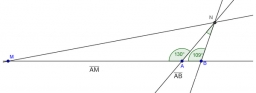
Určte vzdialenosť dvoch miest M, N, medzi ktorými je prekážka, takže miesto N z miesta M nie je viditeľné. Boli merané uhly MAN = 130°, NBM = 109° a vzdialenosti |AM| = 54, |BM| = 60, pričom body A, B, M ležia na jednej priamke.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- priamka
- planimetria
- pravouhlý trojuholník
- trojuholník
- kosínusová veta
- sínusová veta
- goniometria a trigonometria
- sínus
- kosínus
- tangens
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Určte 9
Určte vzdialenosť dvoch neprístupných miest P, Q, ak vzdialenosť dvoch pozorovacích miest A, B je 2000m a ak poznáte veľkosť uhlov QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažované miesta A, B, P, Q ležia v jednej rovine. - Teplota rovnaká
Teploty dvoch miest boli merané súčasne. Teplota v meste A bola 60 stupňov °F a stúpala konštantnou rýchlosťou 2 stupne za hodinu. Teplota v meste B bola 40°F a stúpala konštantnou rýchlosťou 10°F za hodinu Nájdite čas v hodinách, keď je teplota v oboch - V jednej rovine
Mestá A, B, C ležia v jednej výškovej rovine. C je 50 km na východ od B, B je severne od A. C je odchýlené o 50° od A. Lietadlo letí okolo miest A, B, C v rovnakej výške. Keď lietadlo letí okolo B, jeho výškový uhol k A je 12°. Určte výškový uhol k A, keď - V trojuholníku 15
V trojuholníku ABC určte súradnice bodu B, ak viete, že body A, B ležia na priamke 3x-y-5=0, body A, C ležia na priamke 2x+3y+4=0, bod C leží na súradnicovej osi x a uhol pri vrchole C je pravý.
- Kolineárne body
Ukážte, že body A (-1,3), B (3,2), C (11,0) sú kolineárne (ležia na jednej priamke). - Vzdialenosť 15203
V rovine sú dané body A, B a C vzdialené od seba 3 cm, pričom neleží v jednej priamke. Vyznač množinu všetkých bodov, ktorých vzdialenosť je od všetkých troch bodov menšia alebo rovná 2,5 cm. - Priamky 5
Koľkými priamkami možno spojiť 8 bodov, ak tri body ležia na jednej priame a z ostatných žiadne tri neležia na tej istej priamke?
