Vypočítejte 20
Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17 cm, poloměr vepsané kružnice ρ=2 cm.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- PT - poloměr vepsané
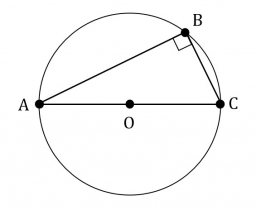
Máme dané strany v pravoúhlém trojúhelníku a = 30 cm, b = 12,5 cm. Pravý úhel je při vrcholu C. Vypočítejte poloměr vepsané kružnice. - Trojúhelník PT
Jedna odvěsna pravoúhlého trojúhelníku ABC má délku a= 14 cm a poloměr kružnice vepsané do tohoto trojúhelníku r= 5 cm. Vypočítejte délku přepony a jeho druhé odvěsny. - Odvěsna a vepsaná kružnice
V pravoúhlém trojúhelníku je dána jedna odvěsna dlouhá 14 cm a poloměr vepsané kružnice 5 cm. Vypočítejte obsah tohoto pravoúhlého trojúhelníku. - RS trojuhélník
Vypočítejte poloměry kružnice vepsané a opsané rovnostrannému trojúhelníku se stranou a=51 cm. - Trojúhelník - parametry
V trojúhelníku ABC známe a = 4 cm, b = 6 cm, γ = 60°. Vypočítejte obsah, poloměr vepsané a opsané kružnice. - PT a kružnice
Řešte pravoúhlý trojúhelník, jsou-li dány poloměry vepsané r=8 a opsané kružnice R=22. - V pravoúhlém 2
V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice).
