Obsah + vyjádření neznámé ze vzorce - příklady a úlohy - strana 17 z 36
Počet nalezených příkladů: 720
- Vypočítejte 4839
 Vypočítejte úhlopříčku takového čtverce, pro který platí, že jeho obsah se rovná jeho obvodu (bez uvažování jednotek, číselně...).
Vypočítejte úhlopříčku takového čtverce, pro který platí, že jeho obsah se rovná jeho obvodu (bez uvažování jednotek, číselně...). - Ohraničují fontanu
 Kolem fontány tvaru kruhu je vybudovaný chodník široký 2m. Poloměry kružnic, které stezka z obou stran ohraničují jsou 4:3. Jakou plochu v metrech čtverečních zabírá tento chodník?
Kolem fontány tvaru kruhu je vybudovaný chodník široký 2m. Poloměry kružnic, které stezka z obou stran ohraničují jsou 4:3. Jakou plochu v metrech čtverečních zabírá tento chodník? - Ornament
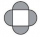 Ornament je složen z jednoho čtverce a čtyř tmavých půlkruhů. Obsah čtverce je 4 cm². Vypočítejte obsah jednoho tmavého půlkruhu a výsledek zaokrouhlete na setiny.
Ornament je složen z jednoho čtverce a čtyř tmavých půlkruhů. Obsah čtverce je 4 cm². Vypočítejte obsah jednoho tmavého půlkruhu a výsledek zaokrouhlete na setiny. - Máme rovnoběžník
 Máme rovnoběžník ABCD, kde AB je 6,2 cm BC je 5,4 cm AC je 4,8 cm vypočítejte výšku na stranu AB a úhel DAB
Máme rovnoběžník ABCD, kde AB je 6,2 cm BC je 5,4 cm AC je 4,8 cm vypočítejte výšku na stranu AB a úhel DAB
- Obdélník 62
 Obdélník má obsah 147 cm². Jedna jeho strana je přitom třikrát delší než druhá strana. Kratší stranu obdélníka zvětšíme o 8 cm. O kolik cm² bude obsah nového obdélníku větší než obsah původního obdelníka?
Obdélník má obsah 147 cm². Jedna jeho strana je přitom třikrát delší než druhá strana. Kratší stranu obdélníka zvětšíme o 8 cm. O kolik cm² bude obsah nového obdélníku větší než obsah původního obdelníka? - Kosočtverec
 Kosočtverec má obsah S = 120 cm2, poměr velikosti jeho úhlopříček e: f = 5:12. Vypočítejte veľlkosť strany a výšky tohoto kosočtverce.
Kosočtverec má obsah S = 120 cm2, poměr velikosti jeho úhlopříček e: f = 5:12. Vypočítejte veľlkosť strany a výšky tohoto kosočtverce. - Obdélník
 Obdélník má jednu stranu o 8 cm menší než druhu. Pokud zmenšíš délku o 6 cm a zvětšíš šířku o 2 cm, dostaneš čtverec, jehož obsah je 400 cm². Jaké jsou původní rozměry obdélníku?
Obdélník má jednu stranu o 8 cm menší než druhu. Pokud zmenšíš délku o 6 cm a zvětšíš šířku o 2 cm, dostaneš čtverec, jehož obsah je 400 cm². Jaké jsou původní rozměry obdélníku? - Čtverec
 Čtverec na obrázku má délku strany a = 20 cm. Obvodové oblouky mají středy ve vrcholech čtverce. Vypočítejte obsah vybarveného útvaru. Vyjádři obsah pomocí strany a.
Čtverec na obrázku má délku strany a = 20 cm. Obvodové oblouky mají středy ve vrcholech čtverce. Vypočítejte obsah vybarveného útvaru. Vyjádři obsah pomocí strany a. - Základny
 Základny rovnoramenného lichoběžníku ABCD mají délky 10 cm a 6 cm. Jeho ramena svírají s delší základnou úhel α = 50˚. Vypočtěte obvod a obsah lichoběžníku ABCD.
Základny rovnoramenného lichoběžníku ABCD mají délky 10 cm a 6 cm. Jeho ramena svírají s delší základnou úhel α = 50˚. Vypočtěte obvod a obsah lichoběžníku ABCD.
- V pravoúhlém 2
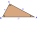 V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice).
V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice). - Pole obdélník
 Pole ve tvaru obdélníka má délku 119 m a šířku 19 m. O kolik se musí zkrátit jeho délka a zvětšit jeho šířka, aby jeho plocha zůstala zachována a jeho obvod se zvětšil o 24 m?
Pole ve tvaru obdélníka má délku 119 m a šířku 19 m. O kolik se musí zkrátit jeho délka a zvětšit jeho šířka, aby jeho plocha zůstala zachována a jeho obvod se zvětšil o 24 m? - Zahrada
 Délky stran obdélníkové zahrady jsou v poměru 1:2. Úhlopříčka má délku 20 metrů. Vypočítejte výměru a obvod zahrady.
Délky stran obdélníkové zahrady jsou v poměru 1:2. Úhlopříčka má délku 20 metrů. Vypočítejte výměru a obvod zahrady. - Délky stran a úhly
 Vypočtěte délky stran a úhly v pravoúhlém trojúhelníku. S = 210, o = 70.
Vypočtěte délky stran a úhly v pravoúhlém trojúhelníku. S = 210, o = 70. - Uhlopříčky kosočtverce
 Vypočítej délky uhlopříček kosočtverce, je-li obsah kosočtverce 156cm čtverečních a délka strany 13cm.
Vypočítej délky uhlopříček kosočtverce, je-li obsah kosočtverce 156cm čtverečních a délka strany 13cm.
- Trojúhelník ABC
 Plocha trojúhelníku je 12 cm čtverečních. Úhel ACB = 30º, AC = (x + 2) cm, BC = x cm. Vypočítejte hodnotu x.
Plocha trojúhelníku je 12 cm čtverečních. Úhel ACB = 30º, AC = (x + 2) cm, BC = x cm. Vypočítejte hodnotu x. - Kosočtverec - úhlopříčky
 V kosočtverci s obsahem 150 cm² je poměr úhlopříček 3:4. Vypočítejte délku jeho výšky.
V kosočtverci s obsahem 150 cm² je poměr úhlopříček 3:4. Vypočítejte délku jeho výšky. - Dlažba
 Kolik Kč zaplatíš za položení dlažby ve čtvercové místnosti s úhlopříčkou 8 m, jestliže m² přijde na 420 Kč?
Kolik Kč zaplatíš za položení dlažby ve čtvercové místnosti s úhlopříčkou 8 m, jestliže m² přijde na 420 Kč? - Pravoúhlý Δ
 Pravoúhlý trojúhelník má délku odvěsny 56 cm a délku přepony 70 cm. Vypočítejte výšku trojúhelníku.
Pravoúhlý trojúhelník má délku odvěsny 56 cm a délku přepony 70 cm. Vypočítejte výšku trojúhelníku. - Pravoúhlý trojúhelník
 Vypočítejte chybějící stranu b a vnitřní úhly, obvod a obsah pravoúhlého trojúhelníku pokud a=10 cm a přepona c = 16 cm.
Vypočítejte chybějící stranu b a vnitřní úhly, obvod a obsah pravoúhlého trojúhelníku pokud a=10 cm a přepona c = 16 cm.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
