Tvar
Určete goniometricky tvar komplexního čísla z=23−10i
Správná odpověď:

Zobrazuji 2 komentáře:
Tipy na související online kalkulačky
Vyzkoušejte také kalkulačku s komplexními čísly.
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Nejpřirozenější aplikací trigonometrie a goniometrických funkcí představuje výpočet trojúhelníků. Běžné i méně běžné výpočty různých typů trojúhelníků nabízí naše trigonometrická kalkulačka trojúhelníku. Slovo trigonometrie pochází z řečtiny a doslovně znamená výpočet trojúhelníku.
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Nejpřirozenější aplikací trigonometrie a goniometrických funkcí představuje výpočet trojúhelníků. Běžné i méně běžné výpočty různých typů trojúhelníků nabízí naše trigonometrická kalkulačka trojúhelníku. Slovo trigonometrie pochází z řečtiny a doslovně znamená výpočet trojúhelníku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- aritmetika
- absolutní hodnota
- planimetrie
- Pythagorova věta
- čísla
- komplexní čísla
- goniometrie a trigonometrie
- tangens
- arkustangens
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Obkladači
 První obkladač by obložil vnitřek bazénu za 5 pracovních hodín, druhý by na stejnou práci potřeboval 7 pracovních hodín. Za kolik hodín by obložili vnitřek bazénu společně, jestliže druhý obkladač začne pracovat na bazénu o 12 minut později něž první?
První obkladač by obložil vnitřek bazénu za 5 pracovních hodín, druhý by na stejnou práci potřeboval 7 pracovních hodín. Za kolik hodín by obložili vnitřek bazénu společně, jestliže druhý obkladač začne pracovat na bazénu o 12 minut později něž první? - Vypočítejte 81606
 Délka jedné ze dvou tětiv kruhu je 12 cm. Pokud jsou akordy vzdáleny 6 cm a 7 cm od středu kruhu, vypočítejte délku druhého akordu.
Délka jedné ze dvou tětiv kruhu je 12 cm. Pokud jsou akordy vzdáleny 6 cm a 7 cm od středu kruhu, vypočítejte délku druhého akordu. - Digitální
 Digitální fotografie má rozměry 640 × 480 pixelů. Který z klasických papírových formátů fotografie je „nejpodobnější": 9 × 6 cm, 10 × 7 cm, 13 × 9 cm, 15 × 10 cm, 18 × 13 cm nebo 30 × 20 cm?
Digitální fotografie má rozměry 640 × 480 pixelů. Který z klasických papírových formátů fotografie je „nejpodobnější": 9 × 6 cm, 10 × 7 cm, 13 × 9 cm, 15 × 10 cm, 18 × 13 cm nebo 30 × 20 cm? - Jiho-západ
 Muž v poušti ujede 8,7 míle ve směru S 26° W (jiho-západ). Potom se otočí o 90° a přejde 9 mil ve směru na N 49° W (severo západně). Jak daleko je v té době od svého výchozího bodu a jeho postoj od jeho výchozího bodu?
Muž v poušti ujede 8,7 míle ve směru S 26° W (jiho-západ). Potom se otočí o 90° a přejde 9 mil ve směru na N 49° W (severo západně). Jak daleko je v té době od svého výchozího bodu a jeho postoj od jeho výchozího bodu?
- Najděte číslo
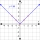 Najděte na číselné ose číslo, jehož vzdálenost od čísla 3 je čtyřikrát menší než od čísla 15 (určete obě řešení).
Najděte na číselné ose číslo, jehož vzdálenost od čísla 3 je čtyřikrát menší než od čísla 15 (určete obě řešení). - Vypočítej: 3
 Vypočítej: |7 − 15| + |8| − |−13| − 1 =
Vypočítej: |7 − 15| + |8| − |−13| − 1 = - Chodník 6
 Chodník kolem domku Vybíralových má dvě části v celkové délce 19 metrů. Delší část chodníku je o 1 metr kratší než trojnásobek délky kratší části chodníku, Rozhodněte o každém z následujících tvrzení, zda je pravdivé, či nikoli. a) Delší část chodníku má
Chodník kolem domku Vybíralových má dvě části v celkové délce 19 metrů. Delší část chodníku je o 1 metr kratší než trojnásobek délky kratší části chodníku, Rozhodněte o každém z následujících tvrzení, zda je pravdivé, či nikoli. a) Delší část chodníku má - Uprostřed 63224
 Na číselné ose je uprostřed mezi číslem 428 a neznámým číslem 290. Zjistíte neznámé číslo.
Na číselné ose je uprostřed mezi číslem 428 a neznámým číslem 290. Zjistíte neznámé číslo. - Určete 20
 Určete velikost úhlu mezi vektory u =(3; -5) a v = (10;6)
Určete velikost úhlu mezi vektory u =(3; -5) a v = (10;6)
- Je dán 15
 Je dán koncový bod vektoru, který je umístěn v počátku kartézské soustavy Oxy. Určete souřadnice vektoru, jeho velikost a načrtněte jej: P[3,4] ; Q[-2,7] ; S[-5,-2] . .. tj. Vektory PO, QO, SO
Je dán koncový bod vektoru, který je umístěn v počátku kartézské soustavy Oxy. Určete souřadnice vektoru, jeho velikost a načrtněte jej: P[3,4] ; Q[-2,7] ; S[-5,-2] . .. tj. Vektory PO, QO, SO - Určete 19
 Určete neznámou souřadnici vektoru tak, aby vektory byly kolineární: e=(7, -2), f = (-2, f2) c= ( -3/7, c2), d=(-4,0)
Určete neznámou souřadnici vektoru tak, aby vektory byly kolineární: e=(7, -2), f = (-2, f2) c= ( -3/7, c2), d=(-4,0) - Orientovanými 55871
 Složte dvě posunutí d1 a d2 znázorněná orientovanými úsečky OA a OB. Souřadnice bodů jsou O=(0m,0m), A=(3m,3m), B=(5m,2m). Změřte velikost výsledného posunutí d.
Složte dvě posunutí d1 a d2 znázorněná orientovanými úsečky OA a OB. Souřadnice bodů jsou O=(0m,0m), A=(3m,3m), B=(5m,2m). Změřte velikost výsledného posunutí d. - Marek 2
 Marek měl 325 Kč. Koupil si za 129 Kč tričko, v rybářských potřebách chtěl utratit 276 Kč. Kolik Kč mu na rybářské potřeby přidali rodiče? Kolik týdnů mu krátili o 10 Kč kapesné, než splatil dluh?
Marek měl 325 Kč. Koupil si za 129 Kč tričko, v rybářských potřebách chtěl utratit 276 Kč. Kolik Kč mu na rybářské potřeby přidali rodiče? Kolik týdnů mu krátili o 10 Kč kapesné, než splatil dluh? - Je dán 13
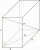 Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH.
Je dán pravidelný čtyřboký hranol ABCDEFGH s podstavnou hranou AB délky 8 cm a výškou 6 cm. Bod M je střed hrany AE. Určete vzdálenost bodu M od roviny BDH.
- Rovnoběžné 45511
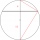 Dvě rovnoběžné tětivy v kružnici o poloměru 6cm mají délky 6cm a 10cm. Vypočítej jejich vzájemnou vzdálenost. Najdi obě řešení.
Dvě rovnoběžné tětivy v kružnici o poloměru 6cm mají délky 6cm a 10cm. Vypočítej jejich vzájemnou vzdálenost. Najdi obě řešení. - Trojnásobek 43541
 Vypočítej trojnásobek absolutní hodnoty rozdílu čísel 3/5 a –1/3.
Vypočítej trojnásobek absolutní hodnoty rozdílu čísel 3/5 a –1/3. - Kolik
 Kolik je takových trojmístných čísel, které nejsou na číselné ose blíže k číslu 600 jako k číslu 400?
Kolik je takových trojmístných čísel, které nejsou na číselné ose blíže k číslu 600 jako k číslu 400?
