Hranol X
Hranol s hranami o dĺžkach x cm, 2x cm a 3x cm a má objem 48000 cm3.
Akú veľkosť má povrch tohto hranola?
Akú veľkosť má povrch tohto hranola?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikastereometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Hranol 4b 3
 Hranol má podstavu štvorca so stranou dlhou 3 cm. Uhlopriečka bočnej steny hranola/BG/je 5 cm. Vypocitajte povrch tohto hranola v cm štvorcových a objem v litroch.
Hranol má podstavu štvorca so stranou dlhou 3 cm. Uhlopriečka bočnej steny hranola/BG/je 5 cm. Vypocitajte povrch tohto hranola v cm štvorcových a objem v litroch. - Povrch 19
 Povrch trojbokého hranola je 157,2 dm2, jeho plášť má obsah 126 dm². Akú plochu zaberie na polici, položený na podstave?
Povrch trojbokého hranola je 157,2 dm2, jeho plášť má obsah 126 dm². Akú plochu zaberie na polici, položený na podstave? - Pravidelný 7
 Pravidelný trojboký hranol je vysoký 7 cm. Jeho podstava je rovnostranný trojuholník, ktorého výška je 3 cm. Vypočítaj povrch a objem tohto hranola.
Pravidelný trojboký hranol je vysoký 7 cm. Jeho podstava je rovnostranný trojuholník, ktorého výška je 3 cm. Vypočítaj povrch a objem tohto hranola. - Vypočítaj 127
 Vypočítaj povrch a objem štvorbokého hranola s lichobežníkovou podstavou, kde a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, va = 3,7 cm a výška hranola h = 5 cm.
Vypočítaj povrch a objem štvorbokého hranola s lichobežníkovou podstavou, kde a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, va = 3,7 cm a výška hranola h = 5 cm. - Hranol - kosodĺžnik
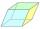 Vypočítajte povrch a objem hranola s telesovou výškou v = 10 cm a s podstavou v tvare kosodĺžnika so stranami a = 5,8 cm, b = 3 cm a vzdialenosťou dvoch jeho dlhších strán w = 2,4 cm.
Vypočítajte povrch a objem hranola s telesovou výškou v = 10 cm a s podstavou v tvare kosodĺžnika so stranami a = 5,8 cm, b = 3 cm a vzdialenosťou dvoch jeho dlhších strán w = 2,4 cm. - Trojboký v3
 Urč objem a povrch trojbokého hranola s výškou 9 cm ak podstava je rovnostranný trojuholník so stranou 8 cm.
Urč objem a povrch trojbokého hranola s výškou 9 cm ak podstava je rovnostranný trojuholník so stranou 8 cm. - Hranol 4b
 Vypočítaj povrch štvorbokého hranola vysokého 2 dm ktoreho podstava je obdĺžnik so stranami 17 cm a 1,3 dm
Vypočítaj povrch štvorbokého hranola vysokého 2 dm ktoreho podstava je obdĺžnik so stranami 17 cm a 1,3 dm
