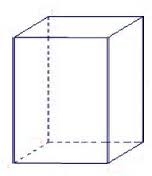
Hranol 4b 3
Hranol má podstavu štvorca so stranou dlhou 3 cm. Uhlopriečka bočnej steny hranola/BG/je 5 cm. Vypočítajte povrch tohto hranola v cm štvorcových a objem v litroch.
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Viete objem a jednotku objemu a chcete premeniť jednotku objemu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
stereometriaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Kolmý hranol
Kolmý hranol leží na podstave v tvare štvorca so stranou dlhou 3 cm. Uhlopriečka bočnej steny hranola u=5 cm. Vypočítajte objem tohto hranola. - Štvorboký 20
Štvorboký hranol má objem 720 cm³. Vypočítajte výšku hranola, ak podstavu tvorí kosodĺžnik so stranou dlhou 16 cm a príslušnou výškou 5 cm. - Objem 35
Objem štvorbokého hranola je 723,6 cm³. Podstavou tohto hranola je kosoštvorec so stranou dlhou 9 cm a príslušnou výškou dlhou 6,7 cm. Zisti výšku hranola. - Podstava 9
Podstava hranola má tvar štvorca so stranou 10 cm. Výška hranola je 20 cm. Vypočítajte výšku ihlana s podstavou tvaru štvorca so stranou 10 cm, ktorý má štyrikrát menší objem ako hranol. - Podstava 10
Podstava hranola má tvar štvorca so stranou 10 cm. Výška hranola je 20 cm. Vypočítajte výšku ihlana s podstavou tvaru štvorca so stranou 10 cm, ktorý má štyrikrát menší objem ako hranol. - Trojuholník skleník
Skleník má tvar hranola položeného na bočnej stene. Podstavu tvorí lichobežník a trojuholník. Dolná základňa lichobežníka má dĺžku 3 m, horná základňa (a strana trojuholníka) má dĺžku 2 m, výška lichobežníka je 1,8 m a výška trojuholníka je 0,6 m. Výška h - Hranol 37
Hranol má štvorcovú podstavu s hranou dlhou 5 cm a výšku 20 cm. Vypočítaj jeho: a) obsah podstavy b) obvod podstavy c) objem d) povrch
