Splav
Splav na umývanie repy má tvar hranola s podstavou rovnoramenného trojuholníka, ktorého základňa je 6,8 m ( šírka splavu) a výška 4,8 m (hĺbka splavu, výška trojuholníka). Splav je dlhý 35 m (výška hranola). Vypočítajte objem splavu!
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Trojboký hranol
Vypočítaj objem a povrch trojbokého hranola ABCDEF s podstavou rovnoramenného trojuholníka. Základňa podstavy je 16 cm, rameno 10 cm, vc = 6 cm. Výška hranola je 9 cm. - Kachlička
Kachlička má tvar rovnoramenného trojuholníka, ktorého základňa má dĺžku 4 cm a k nej prislúchajúca výška má dĺžku 6 cm. Najmenej koľko kachličiek treba na pokrytie steny s obsahom 2,4 m2 - Trojboký hranol
Pravidelný trojboký hranol má podstavu v tvare rovnoramenného trojuholníka o základni o základni 86 mm a ramenách 6,4 cm, Výška hranola je 24 cm. Vypočítajte objem. - Vypočítajte 29 Vypočítajte objem a povrch hranola, ktorého výška je 16 cm a podstava má tvar pravouhlého trojuholníka s odvesnami 5 cm a 12 cm a preponou 13 cm.
- Základňa
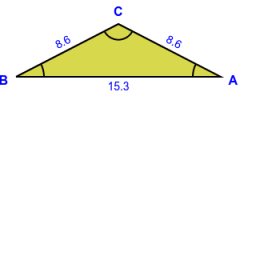
Vypočítaj veľkosť základne rovnoramenného trojuholníka, ktorého výška k základni má veľkosť 5 cm a dĺžka ramena je 6,5 cm. Aký je obvod tohto trojuholníka? - Trojboký hranol
Vypočítaj povrch a objem trojbokého hranola s podstavou tvaru pravouhlého trojuholníka, ak a=3 cm, b=4 cm, c=5 cm a výška hranola v=12 cm. - RRT hranol
Podstava kolmého hranola je rovnoramenný trojuholník, ktorého základňa je 10 cm a rameno 13 cm. Výška hranola je trojnásobok výšky podstavného trojuholníka na jeho základňu. Vypočítajte povrch hranola.
