Z7–I–2 MO 2017
Dané sú dve dvojice rovnobežných priamok AB k CD a AC k BD. Bod E leží na priamke BD, bod F je stredom úsečky BD, bod G je stredom úsečky CD a obsah trojuholníka ACE je 20 cm2.
Určte obsah trojuholníka DFG.
Určte obsah trojuholníka DFG.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
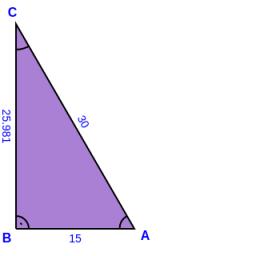
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaalgebraplanimetriaJednotky fyzikálnych veličíntémaÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Uhlopriečka obdĺžnika
 Bod B je vrchol obdĺžnika ABCD. Na priamke leží uhlopriečka BD tohto obdĺžnika. Bod X je vnútorný bod strany AD obdĺžnika ABCD a bod Y vnútorný bod strany CD. Zostrojte chýbajúce vrcholy D, A, C obdĺžnika ABCD.
Bod B je vrchol obdĺžnika ABCD. Na priamke leží uhlopriečka BD tohto obdĺžnika. Bod X je vnútorný bod strany AD obdĺžnika ABCD a bod Y vnútorný bod strany CD. Zostrojte chýbajúce vrcholy D, A, C obdĺžnika ABCD. - C-I-2 2018 MO
 Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr
Na strane AB trojuholníka ABC sú dané body D a E tak, že |AD| = |DE| = |EB|. Body A a B sú postupne stredmi úsečiek CF a CG. Priamka CD pretína priamku FB v bode I a priamka CE pretína priamku AG v bode J. Dokážte, že priesečník priamok AI a BJ leží na pr - Trojuholník ABC
 V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC.
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Vo štvorci
 Vo štvorci ABCD leží bod X na uhlopriečke AC. Dĺžka úsečky XC je trojnásobkom dĺžky úsečky AX. Bod S je stredom strany AB. Dĺžka strany AB je 1 cm. Aká je dĺžka úsečky XS?
Vo štvorci ABCD leží bod X na uhlopriečke AC. Dĺžka úsečky XC je trojnásobkom dĺžky úsečky AX. Bod S je stredom strany AB. Dĺžka strany AB je 1 cm. Aká je dĺžka úsečky XS? - Na kružnici
 Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC.
Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC. - Z9 – I – 2 MO 2018
 V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM. - Z8–I–5 MO 2019
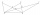 Pre osem navzájom rôznych bodov ako na obrázku platí, že body C, D, E ležia na priamke rovnobežnej s priamkou AB, F je stredom úsečky AD, G je stredom úsečky AC a H je priesečníkom priamok AC a BE. Obsah trojuholníka BCG je 12 cm² a obsah štvoruholníka DF
Pre osem navzájom rôznych bodov ako na obrázku platí, že body C, D, E ležia na priamke rovnobežnej s priamkou AB, F je stredom úsečky AD, G je stredom úsečky AC a H je priesečníkom priamok AC a BE. Obsah trojuholníka BCG je 12 cm² a obsah štvoruholníka DF
