V rovnobežníku 2
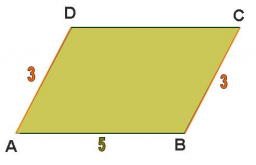
V rovnobežníku je súčet dĺžok strán a+b = 234. Uhol zovretý stranami a a b je 60°. Dĺžka uhlopriečky proti danému uhlu 60° je u=162. Vypočítajte strany rovnobežníka, jeho obvod a obsah.
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Rovnobežník - uhlopriečky
Vypočítajte obsah rovnobežníka, ak sú veľkosti strán a=80, b=60 a veľkosť uhla zovretého uhlopriečkami je 60°. - Trojuholník SUS
Vypočítajte plochu a obvod trojuholníka, ak jeho dve strany sú dlhé 121 mm a 118 mm a uhol nimi zovretý je 60°. - Vypočítajte 67
Vypočítajte obsah rovnobežníka so stranami a=25,3 b=13,8 a uhol zavretý stranami je a=72° - Pole
Pole má tvar rovnobežníka s rozmermi a=67 m a prislúchajúcou výškou 219 m. Dve a dve strany zvierajú uhol 67°. Vypočítajte výmeru pola v hektároch. - SUS trojuholník
V trojuholníku sú dané dve strany dlhé 19 a 20 a uhol nimi zovretý 124°54'. Vypočítajte obsah tohto trojuholníka. - Strany
Strany rovnobežníka sú 8 a 6 (cm), odchýlka uhlopriečok je 60°. Aký je jeho obsah? - Štvoruholníky
Ktoré z nasledujúcich tvrdení o uhloch v štvoruholníkoch je nepravdivé a. V pravouhlom lichobežníku je práve jeden vnútorný uhol tupý. b. Uhlopriečky kosoštvorca zvierajú pravý uhol. c. Súčet veľkostí ľubovoľných dvoch vnútorných uhlov v rovnobežníku je 1
