Rovnobežník - uhlopriečky
Vypočítajte obsah rovnobežníka, ak sú veľkosti strán a=80, b=60 a veľkosť uhla zovretého uhlopriečkami je 60°.
Vaša odpoveď:
Vaša odpoveď:
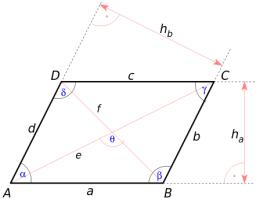
Zobrazujem 1 komentár:
Kristián
Vypočítajte obsah rovnobežníka so stranami a=25,3 b=13,8 a uhol zavretý stranami je a=72°
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Ťažisko a obsah
V trojuholníku ABC sú dané dĺžky jeho ťažníc tc=9, ta=6. Označme T priesečník ťažníc, S stred strany BC. Veľkosť uhla CTS je 60°. Vypočítajte dĺžku strany BC s presnosťou na 2 desatinné miesta - Štvoruholník - uhly
Výpočty z geometrie: Pomery strán štvoruholníka sú 3:6:4,5:3,5. Vypočítajte ich dĺžky, ak obvod je 51 cm. Veľkosti uhlov v štvoruholníku sú = 29°30', = 133°10',= 165°20'. Aká je veľkosť uhla D? - Susedné uhly 3
Uhly alfa a beta sú susedné . Vypočítajte veľkosť uhla beta ak alfa sa rovná 57°. - V trojuholníku
V trojuholníku ABC sa veľkosť vnútorného uhla gama rovná tretine vnútorného uhla alfa. Veľkosť vnútorného uhla beta je o 80 stupňov väčší ako veľkosť uhla gama. Vypočítajte veľkosti vnútorných uhlov trojuholníka ABC. - Trojuholník radiány
Veľkosti dvoch vnútorných uhlov trojuholníku ABC sú α=6/18π and β=7/18π. Vypočítajte veľkosť tretieho uhla. - Vypočítajte 62
Vypočítajte obsah rovnoramenného lichobežníka ABCD, ak a =14 cm, c= 8 cm a veľkosť uhla DAB je 52°. - Uhly kosoštvorca
Ak je jeden uhol v kosoštvorci rovný 73,8°, aký veľký je k nemu susedný uhol kosoštvorca?
