Z9 – I – 5 MO 2018

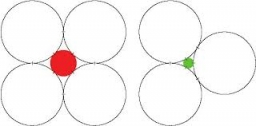
Peter a Ivan vytvárali dekorácie z navzájom zhodných bielych kruhov. Peter použil štyri kruhy, ktoré položil tak, že sa každý dotýkal dvoch iných kruhov. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých štyroch bielych kruhov, a ten vyfarbil červenou.

Ivan použil tri kruhy, ktoré položil tak, že sa dotýkali navzájom. Medzi ne potom vložil iný kruh, ktorý sa dotýkal všetkých troch bielych kruhov, a ten vyfarbil zelenou. Ivan si všimol, že jeho zelený kruh a Petrov červený kruh sú rôzne veľké, a tak začali spolu zisťovať, ako sa líšia.

Vyjadrite polomery červeného a zeleného kruhu všeobecne pomocou polomeru bielych kruhov.

Správna odpoveď:

r₁ = (sqrt(2)-1) * r
r₂ = r( fr(2,3) * sqrt(3) - 1)

Postup správneho riešenia:

$$\begin{gathered} (2r{)}^2+(2r{)}^2=(r+2r_1+r{)}^2 \\ 4r^2+4r^2=(2r+2r_1{)}^2 \\ 8r^2=(2r+2r_1{)}^2 \\ r\sqrt{8}=2r+2r_1 \\ {r}_1=(\sqrt{2}-1)\cdot r \end{gathered}$$

$$\begin{gathered} a=2r \\ h=\sqrt{3}/2\cdot a=\sqrt{3}\cdot r \\ 2/3h=r+r_2 \\ {r}_2=2/3\sqrt{3}\cdot r-r \\ {r}_2=r(\frac{2}{3}\cdot \sqrt{3}-1) \end{gathered}$$

Skúsiť iný príklad