Chovprodukt
Z chovproduktu (Zverimexu) vypredávali rybky z jedného akvária. Ondrej chcel polovicu všetkých rybiek, ale aby nemuseli žiadnu rybku rezať, dostal o polovicu rybky viac, ako požadoval. Matej si prial polovicu zvyšných rybiek, ale rovnako ako Ondrej dostal o polovicu rybky viac než požadoval. Nakoniec Petrik chcel polovicu zvyšných rybiek, ale tiež dostal o polovicu rybky viac než požadoval. Potom bolo akvárium bez rybiek. Koľko rybiek bolo pôvodne v akváriu a koľko ich dostal Ondrej, koľko Matej a koľko Petrík?
Správna odpoveď:

Zobrazujem 1 komentár:
Mo-radce
Možné riešenie. Budeme uvažovať odzadu:
Petrík dostal o polovicu rybky viac, než bola polovica všetkých rybiek, ktoré zostali po Matejovi. Pretože potom bolo akvárium prázdne, bola ona polovica rybky navyše práve polovicou toho, čo zostalo po Matejovi. Po Matejová nákupe teda zostala v akváriu jedna rybka. Matej dostal o polovicu rybky viac, než bola polovica všetkých rybiek, ktoré zostali po Ondrejovi. Pretože potom zostala v akváriu jedna rybka, bola táto rybka a polovica rybky navyše práve polovicou toho, čo zostalo po Ondrejovi. Po Ondrejove nákupu ostali v akváriu tri rybky. Ondrej dostal o polovicu rybky viac, než bola polovica všetkých rybiek, ktoré boli pôvodne v akváriu. Pretože potom ostali v akváriu tri rybky, boli tieto tri rybky a polovica rybky navyše práve polovicou pôvodného množstva rybiek. Pôvodne bolo v akváriu sedem rybek. Teda Ondrej dostal štyri rybky, Matej dve a Petřík jednu rybku.
Iné riešenie:
Ak pôvodný počet rybiek v akváriu označíme x, potom môžeme ďalšie počty postupne vyjadriť takto:
meno dostal zostalo
Ondrej (x + 1) / 2 (x - 1) / 2
Matej (x + 1) / 4 (x - 3) / 4
Petrík (x + 1) / 8 (x - 7) / 8
Odtiaľ je zrejmé, že po Petríkovom nákupe mohlo byť akvárium bez rybiek práve vtedy, keď x = 7. Dosadením ľahko určíme počty rybiek, ktoré si odniesli jednotliví chlapci.
Petrík dostal o polovicu rybky viac, než bola polovica všetkých rybiek, ktoré zostali po Matejovi. Pretože potom bolo akvárium prázdne, bola ona polovica rybky navyše práve polovicou toho, čo zostalo po Matejovi. Po Matejová nákupe teda zostala v akváriu jedna rybka. Matej dostal o polovicu rybky viac, než bola polovica všetkých rybiek, ktoré zostali po Ondrejovi. Pretože potom zostala v akváriu jedna rybka, bola táto rybka a polovica rybky navyše práve polovicou toho, čo zostalo po Ondrejovi. Po Ondrejove nákupu ostali v akváriu tri rybky. Ondrej dostal o polovicu rybky viac, než bola polovica všetkých rybiek, ktoré boli pôvodne v akváriu. Pretože potom ostali v akváriu tri rybky, boli tieto tri rybky a polovica rybky navyše práve polovicou pôvodného množstva rybiek. Pôvodne bolo v akváriu sedem rybek. Teda Ondrej dostal štyri rybky, Matej dve a Petřík jednu rybku.
Iné riešenie:
Ak pôvodný počet rybiek v akváriu označíme x, potom môžeme ďalšie počty postupne vyjadriť takto:
meno dostal zostalo
Ondrej (x + 1) / 2 (x - 1) / 2
Matej (x + 1) / 4 (x - 3) / 4
Petrík (x + 1) / 8 (x - 7) / 8
Odtiaľ je zrejmé, že po Petríkovom nákupe mohlo byť akvárium bez rybiek práve vtedy, keď x = 7. Dosadením ľahko určíme počty rybiek, ktoré si odniesli jednotliví chlapci.
Tipy na súvisiace online kalkulačky
Chcete zaokrúhliť číslo?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Šimon
 Akvárium v tvare kvádra je vysoké 40cm, dno má rozmery 70cm a 50cm. Šimon chcel vytvoriť rybičkám zaujímavé prostredie, tak im na dno pripevnil tri stĺpy. Všetky majú tvar kvádra so štvorcovou podstavou. Podstavná hrana každého kvádra má dĺžku 10cm. Výšky
Akvárium v tvare kvádra je vysoké 40cm, dno má rozmery 70cm a 50cm. Šimon chcel vytvoriť rybičkám zaujímavé prostredie, tak im na dno pripevnil tri stĺpy. Všetky majú tvar kvádra so štvorcovou podstavou. Podstavná hrana každého kvádra má dĺžku 10cm. Výšky - Zvolen - BB
 Matej denne dochádza do Bankej Bystrice, väčšinou chodí vlakom zo Zvolena, ale minule sa mu stalo, že ho vo vlaku uštipla včela. Možno si myslíte, že je celkom nepravdepodobné a Matej si to mysli tiež. Preto by od vás chcel, aby ste mu pomohli. Medzi Zvol
Matej denne dochádza do Bankej Bystrice, väčšinou chodí vlakom zo Zvolena, ale minule sa mu stalo, že ho vo vlaku uštipla včela. Možno si myslíte, že je celkom nepravdepodobné a Matej si to mysli tiež. Preto by od vás chcel, aby ste mu pomohli. Medzi Zvol - Požadované 25461
 Martin sa chcel s otcovou pomôcť zlepiť akvárium. V príručke sa dočítal že by malo mať objem 45 litrov. na stolíku ale nemal veľa miesta dno akvária mohlo mať rozmery iba 25 cm a 40 cm. Ako musí byť akvárium vysoké, aby sa do neho zmestilo požadované množ
Martin sa chcel s otcovou pomôcť zlepiť akvárium. V príručke sa dočítal že by malo mať objem 45 litrov. na stolíku ale nemal veľa miesta dno akvária mohlo mať rozmery iba 25 cm a 40 cm. Ako musí byť akvárium vysoké, aby sa do neho zmestilo požadované množ - Štyri
 Štyri piráti si medzi seba rozdelili 65 mincí. Zoradili sa podľa veku, najmladší dostal najmenej mincí, každý potom o polovicu viac ako predchádzajúci. Koľko mincí dostal najstarší pirát?
Štyri piráti si medzi seba rozdelili 65 mincí. Zoradili sa podľa veku, najmladší dostal najmenej mincí, každý potom o polovicu viac ako predchádzajúci. Koľko mincí dostal najstarší pirát?
- Otec chcel
 Otec chcel pôvodne rozdeliť finančný obnos svojim synom v pomere 7:6. Potom ho však rozdelil v pomere 6:5 (v rovnakom poradí). Jeden zo synov sa rozhneval, že mal pôvodne dostať o 120 eur viac. Koľko eur dostal každý syn?
Otec chcel pôvodne rozdeliť finančný obnos svojim synom v pomere 7:6. Potom ho však rozdelil v pomere 6:5 (v rovnakom poradí). Jeden zo synov sa rozhneval, že mal pôvodne dostať o 120 eur viac. Koľko eur dostal každý syn? - Rybky
 Mišo si kúpil akvárium v tvare kvádra s rozmermi dna 30 cm x 15 cm a výškou 20 cm. Predavač mu odporučil, aby akvárium napĺňal vodou len do výšky 15 cm. Koľko si môže kúpiť najviac mečúňov Mišo do akvária, ak vie, že pre správny život potrebuje mečúň 0,5
Mišo si kúpil akvárium v tvare kvádra s rozmermi dna 30 cm x 15 cm a výškou 20 cm. Predavač mu odporučil, aby akvárium napĺňal vodou len do výšky 15 cm. Koľko si môže kúpiť najviac mečúňov Mišo do akvária, ak vie, že pre správny život potrebuje mečúň 0,5 - Presnosťou 26881
 Anička s Emou piekli spoločne koláče. Ema upiekla o tretinu viac koláčov ako Anička. Anička si nechala tretinu koláčov, Ema si z koláčov, ktoré upiekla, nechala polovicu. Zvyšných 12 koláčov dali rodičom. 1) Určite, koľko koláčov celkom Anička s Emou upie
Anička s Emou piekli spoločne koláče. Ema upiekla o tretinu viac koláčov ako Anička. Anička si nechala tretinu koláčov, Ema si z koláčov, ktoré upiekla, nechala polovicu. Zvyšných 12 koláčov dali rodičom. 1) Určite, koľko koláčov celkom Anička s Emou upie - Neutratených 5855
 Tereza si mesačne zarobí o 50% viac, než utratí. Patrícia si zarobí rovnako ako Tereza, ale utratí o 20% menšiu čiastku, než utratí Tereza. Z neutratených peňazí posiela mesačne každá z nich pätinu na konto detského domova. O koľko percent vyššiu alebo ni
Tereza si mesačne zarobí o 50% viac, než utratí. Patrícia si zarobí rovnako ako Tereza, ale utratí o 20% menšiu čiastku, než utratí Tereza. Z neutratených peňazí posiela mesačne každá z nich pätinu na konto detského domova. O koľko percent vyššiu alebo ni - Orieškov 3279
 Keby som mal o polovicu orechov viac ako mám teraz, mal by som rovnako ako Vendulka. Keby mala Vendulka o tretinu menej ako má teraz, mala by rovnako ako ja. Keby mala o šestinu menej ako má a dala by mi tú časť, mali by sme rovnako. Koľko má orieškov Mat
Keby som mal o polovicu orechov viac ako mám teraz, mal by som rovnako ako Vendulka. Keby mala Vendulka o tretinu menej ako má teraz, mala by rovnako ako ja. Keby mala o šestinu menej ako má a dala by mi tú časť, mali by sme rovnako. Koľko má orieškov Mat
- V činžiaku
 V činžiaku žije 208 ľudí. Žien je tam toľko, ako mužov, ale detí je o 22 viac ako žien. Koľko dospelých žije v činžiaku?
V činžiaku žije 208 ľudí. Žien je tam toľko, ako mužov, ale detí je o 22 viac ako žien. Koľko dospelých žije v činžiaku? - Vypočítaj 22263
 Akvárium má tvar gule s priemerom 36 cm. Odhadni a potom vypočítaj, koľko litrov vody sa zmestí do akvária, keď ich naplníme až po okraj?
Akvárium má tvar gule s priemerom 36 cm. Odhadni a potom vypočítaj, koľko litrov vody sa zmestí do akvária, keď ich naplníme až po okraj? - Na obrázku 5
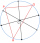 Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a
Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a - Štvorcových 8385
 Martin si chcel s otcovou pomocou zlepiť akvárium. V príručke sa dočítal, že by malo mať objem 45 litrov. Na stolíku nemal veľa miesta. Dno akvária mohlo mať rozmery iba 25 cm a 40 cm. Ako musí byť akvárium vysoké, aby sa do neho zmestilo požadované množs
Martin si chcel s otcovou pomocou zlepiť akvárium. V príručke sa dočítal, že by malo mať objem 45 litrov. Na stolíku nemal veľa miesta. Dno akvária mohlo mať rozmery iba 25 cm a 40 cm. Ako musí byť akvárium vysoké, aby sa do neho zmestilo požadované množs - V akváriu
 V akváriu s dĺžkou 2m, šírkou 1,5m a hĺbkou 2,5m siaha voda do výšky troch štvrtín hĺbky. Môžme do akvária vložiť kamene s objemom 2m kubicke bez toho, aby sa z neho voda vyliala? (0 = Nie, 1 = Áno)
V akváriu s dĺžkou 2m, šírkou 1,5m a hĺbkou 2,5m siaha voda do výšky troch štvrtín hĺbky. Môžme do akvária vložiť kamene s objemom 2m kubicke bez toho, aby sa z neho voda vyliala? (0 = Nie, 1 = Áno)
- Havrany
 Na dvoch stromoch sedelo 17 havranov. Ak z prvého preleteli na druhý strom 3 havrany a z druhého stromu ich 5 odletelo, zostalo na prvom strome 2krát viac havranov než na druhom. Koľko bolo pôvodne havranov na každom strome?
Na dvoch stromoch sedelo 17 havranov. Ak z prvého preleteli na druhý strom 3 havrany a z druhého stromu ich 5 odletelo, zostalo na prvom strome 2krát viac havranov než na druhom. Koľko bolo pôvodne havranov na každom strome? - Akvárium 3
 Do akvária s rozmermi dna 20 cm x 20 cm a výškou 25 cm sme naliali 1 liter vody. Do akej výšky siaha voda v akváriu?
Do akvária s rozmermi dna 20 cm x 20 cm a výškou 25 cm sme naliali 1 liter vody. Do akej výšky siaha voda v akváriu? - Výherného
 Výherného zájazdu do Paríža sa zúčastnilo 48 osôb. Rodinných príslušníkov bolo o 4 viac než osôb, ktoré zájazd vyhrali. Osôb, ktoré síce zájazd nevyhrali, ale zájazd si od niektorého z výhercov odkúpili, bolo o 6 menej ako polovica cestujúcich v autobuse.
Výherného zájazdu do Paríža sa zúčastnilo 48 osôb. Rodinných príslušníkov bolo o 4 viac než osôb, ktoré zájazd vyhrali. Osôb, ktoré síce zájazd nevyhrali, ale zájazd si od niektorého z výhercov odkúpili, bolo o 6 menej ako polovica cestujúcich v autobuse.
