Súčet uhlov
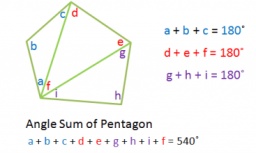
Dokážte, že súčet veľkostí všetkých vnútorných uhlov ľubovoľného konvexného n-uholníka sa rovná (n-2).180 stupňov.
Správna odpoveď:
Zobrazujem 1 komentár:
Dr Math
n-úholník (polygón) možno rozdeliť na n - 2 trojuholníkov. Pretože súčet uhlov trojuholníka je 180°, súčet uhlov polygónu je 180°(n-2).
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Jednotky fyzikálnych veličín:
Téma:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- N-uholník uhly
 Aký je súčet vnútorných uhlov ľubovoľného 7-uholníka? Aký je vnútorný uhol pravidelného konvexného 7-uholníka?
Aký je súčet vnútorných uhlov ľubovoľného 7-uholníka? Aký je vnútorný uhol pravidelného konvexného 7-uholníka? - Pre súčet
 Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°?
Pre súčet s veľkostí vnútorných uhlov mnohouholníka, kde n je počet jeho strán, platí vzťah s=(n−2)⋅180 stupňov. Koľko strán má mnohouholník, ak súčet veľkostí jeho vnútorných uhlov je 900°? - V trojuholníku
 V trojuholníku ABC sa veľkosť vnútorného uhla gama rovná tretine vnútorného uhla alfa. Veľkosť vnútorného uhla beta je o 80 stupňov väčší ako veľkosť uhla gama. Vypočítajte veľkosti vnútorných uhlov trojuholníka ABC.
V trojuholníku ABC sa veľkosť vnútorného uhla gama rovná tretine vnútorného uhla alfa. Veľkosť vnútorného uhla beta je o 80 stupňov väčší ako veľkosť uhla gama. Vypočítajte veľkosti vnútorných uhlov trojuholníka ABC. - Trojuholníka 4050
 Vypočítajte veľkosť vnútorných uhlov trojuholníka, ak je veľkosť druhého uhla o 120 stupňov menšia ako dvojnásobok veľkosti prvého uhla a veľkosť tretieho uhla sa rovná rozdielu veľkostí prvého a druhého uhla.
Vypočítajte veľkosť vnútorných uhlov trojuholníka, ak je veľkosť druhého uhla o 120 stupňov menšia ako dvojnásobok veľkosti prvého uhla a veľkosť tretieho uhla sa rovná rozdielu veľkostí prvého a druhého uhla.
- Dvojnásobkom 83240
 V trojuholníku ABC je veľkosť vnútorného uhla beta dvojnásobkom veľkosti uhla alfa a veľkosti uhla gama je o 20 stupňov menšia ako veľkosť uhla beta. Urči veľkosť všetkých vnútorných uhlov tohto trojuholníka.
V trojuholníku ABC je veľkosť vnútorného uhla beta dvojnásobkom veľkosti uhla alfa a veľkosti uhla gama je o 20 stupňov menšia ako veľkosť uhla beta. Urči veľkosť všetkých vnútorných uhlov tohto trojuholníka. - Štvoruholníky
 Ktoré z nasledujúcich tvrdení o uhloch v štvoruholníkoch je nepravdivé a. V pravouhlom lichobežníku je práve jeden vnútorný uhol tupý. b. Uhlopriečky kosoštvorca zvierajú pravý uhol. c. Súčet veľkostí ľubovoľných dvoch vnútorných uhlov v rovnobežníku je 1
Ktoré z nasledujúcich tvrdení o uhloch v štvoruholníkoch je nepravdivé a. V pravouhlom lichobežníku je práve jeden vnútorný uhol tupý. b. Uhlopriečky kosoštvorca zvierajú pravý uhol. c. Súčet veľkostí ľubovoľných dvoch vnútorných uhlov v rovnobežníku je 1 - Vnútorné uhly
 Vypočítaj zvyšné vnútorné a vonkajšie uhly trojuholníka, ak poznáš vnútorný uhol γ(gama)=34 stupňov a vonkajší uhol 78 stupňov a 40´. Napíš o aký trojuholník ide podľa veľkosti vnútorných uhlov.
Vypočítaj zvyšné vnútorné a vonkajšie uhly trojuholníka, ak poznáš vnútorný uhol γ(gama)=34 stupňov a vonkajší uhol 78 stupňov a 40´. Napíš o aký trojuholník ide podľa veľkosti vnútorných uhlov. - Vo štvoruholníku
 Vo štvoruholníku ABCD, ktorého vrcholy ležia na danej kružnici, je uhol pri vrchole A rovný 58 stupňov a uhol pri vrchole B 134 stupňov. Vypočítajte veľkosti zvyšných vnútorných uhlov.
Vo štvoruholníku ABCD, ktorého vrcholy ležia na danej kružnici, je uhol pri vrchole A rovný 58 stupňov a uhol pri vrchole B 134 stupňov. Vypočítajte veľkosti zvyšných vnútorných uhlov. - Deväťuholník
 Súčet veľkosti vnútorných uhlov deväťuholníka je:
Súčet veľkosti vnútorných uhlov deväťuholníka je:
- Vidieť harmonický
 Je pravda že veľkosť strednej priečky ľubovoľného lichobežníka je harmonickým priemerom veľkostí jeho základní? Dokážte to. Strednej priečka prechádza priesečníkom jeho uhlopriečok a je rovnobežná so základňami.
Je pravda že veľkosť strednej priečky ľubovoľného lichobežníka je harmonickým priemerom veľkostí jeho základní? Dokážte to. Strednej priečka prechádza priesečníkom jeho uhlopriečok a je rovnobežná so základňami. - Rovnoramenný lichobežník 2
 Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných
Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných - Obsah a uhly
 Vypočítajte veľkosti všetkých strán a vnútorných uhlov trojuholníka ABC, ak je dané: S = 501,9; α = 15°28 'a β = 45°.
Vypočítajte veľkosti všetkých strán a vnútorných uhlov trojuholníka ABC, ak je dané: S = 501,9; α = 15°28 'a β = 45°. - Na kruhovom 2
 Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2,5,9, čím vznikne trojuholník. Vypočítajte veľkosti všetkých vnútorných uhlov.
Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2,5,9, čím vznikne trojuholník. Vypočítajte veľkosti všetkých vnútorných uhlov. - Uhly
 V trojuholníku ABC je vnútorný uhol pri vrchole B o 10 stupňov väčší ako uhol pri vrchole A a uhol pri vrchole C je trikrát väčší ako uhol pri vrchole B. Vypočítajte veľkosti vnútorných uhlov trojuholníka.
V trojuholníku ABC je vnútorný uhol pri vrchole B o 10 stupňov väčší ako uhol pri vrchole A a uhol pri vrchole C je trikrát väčší ako uhol pri vrchole B. Vypočítajte veľkosti vnútorných uhlov trojuholníka.
- Alfa, beta, gama
 V trojuholníku ABC je veľkosť vnútorného uhla BETA o 8 stupňov väčšia ako veľkosť vnútorného ALFA uhla a veľkosť vnútorného uhla GAMA je dvakrát väčšia ako veľkosť uhla BETA. Určte veľkosti vnútorných uhlov trojuholníka ABC.
V trojuholníku ABC je veľkosť vnútorného uhla BETA o 8 stupňov väčšia ako veľkosť vnútorného ALFA uhla a veľkosť vnútorného uhla GAMA je dvakrát väčšia ako veľkosť uhla BETA. Určte veľkosti vnútorných uhlov trojuholníka ABC. - Na kruhovom
 Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2, 9,11 čím vznikne trojuholník. vypočítajte veľkosti všetkých vnútorných uhlov toho trojuholníka.
Na kruhovom ciferníku hodín navzájom pospájame body prislúchajúce číslam 2, 9,11 čím vznikne trojuholník. vypočítajte veľkosti všetkých vnútorných uhlov toho trojuholníka. - Trojuholníka 13541
 Uhol alfa je dvakrát väčší ako uhol beta a uhol gama je trikrát väčší ako uhol beta. Určite veľkosti všetkých vnútorných uhlov alfa, beta, gama trojuholníka ABC.
Uhol alfa je dvakrát väčší ako uhol beta a uhol gama je trikrát väčší ako uhol beta. Určite veľkosti všetkých vnútorných uhlov alfa, beta, gama trojuholníka ABC.
