Pravouhlý
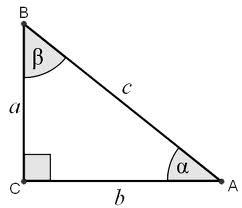
Určete úhly pravoúhlého trojúhelníku, s přeponou c a odvěsnami a, b; jestliže platí:
2a+5b=5,283c
Vaše odpověď:
2a+5b=5,283c
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriezákladní operace a pojmygoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Pravoúhlý trojúhelník FGH
V pravoúhlém trojúhelníku s odvěsnami f a g a přeponou h, jestliže f = 7 cm a h = 11,2 cm, jaké je g? - Objem tříbokého hranolu
Jaký je objem trojbokého hranolu s podstavou pravoúhlého trojúhelníku s odvěsnami 6 dm a 8 dm a přeponou 10 dm a výška hranolu je 40 dm? - Trojboký hranol
Vypočítejte objem a povrch hranolu, jehož výška je 16 cm a podstava má tvar pravoúhlého trojúhelníku s odvěsnami 5 cm a 12 cm a přeponou 13 cm. - Kosinus
Určete kosinus nejmenšího vnitřního úhlu v pravoúhlém trojúhelníku s odvěsnami 3 a 8 a přeponou 8,544. - Trojúhelník PT
Vypočítejte obsah pravoúhlého trojúhelníku ABC s odvěsnami a=15 cm, b=1,7 dm. - Vektory
Pro vektor w platí: w = +4v. UrčPro vektor w platí: w = +4v. Určete souřadnice vektoru w, jestliže u=(-4, 2), v=(0, 3) - Trojúhelník
Narysuj pravoúhlý trojúhelník ABC, ve kterém platí: |AB| = 5 cm, |BC| = 3 cm, |AC| = 4 cm. Zostroj Thaletovu kružnici nad přeponou trojúhelníku ABC.
