Patří - leží
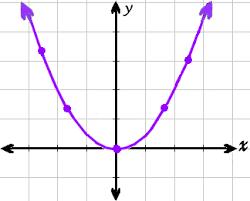
Napište rovnici kvadratické funkce níž patří body A (-1, 10), B (2, 19), C (1,4)
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Lichoběžníku 44431
 1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky
1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky - Souřadnicovými 82580
 Napište rovnici elipsy, která prochází body a její osy jsou totožné se souřadnicovými osami, když: A = [2, 3] a B = [−1, −4].
Napište rovnici elipsy, která prochází body a její osy jsou totožné se souřadnicovými osami, když: A = [2, 3] a B = [−1, −4]. - Paraboly 80525
 Napište rovnici paraboly, která prochází body: A[1,1] B[3,-1] C[1,2]
Napište rovnici paraboly, která prochází body: A[1,1] B[3,-1] C[1,2] - Procházela 11311
 Čára procházela třemi body - viz tabulka: x y -6 4 -4 3 -2 2 Napište přímkovou rovnici ve tvaru y=mx+b.
Čára procházela třemi body - viz tabulka: x y -6 4 -4 3 -2 2 Napište přímkovou rovnici ve tvaru y=mx+b.
- Napište 3
 Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0.
Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0. - Obecná rovnice
 Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná
Ve všech příkladech napište OBECNOU ROVNICI přímky, která je nějakým způsobem zadána. A)přímka je dána parametricky: x = - 4 + 2p;y = 2 - 3p B) přímka je dána směrnicově: y = 3x - 1 C) přímka je dána dvěma body: A [3; -3], B [-5; 2] D) přímka protíná - Kořeny
 Určitě v kvadratické rovnici absolutní člen q tak, aby rovnice měla reálný dvojnásobný kořen a tento kořen x vypočítejte: 5x ² +9x + q = 0
Určitě v kvadratické rovnici absolutní člen q tak, aby rovnice měla reálný dvojnásobný kořen a tento kořen x vypočítejte: 5x ² +9x + q = 0 - Rovnice hyperboly
 Napište rovnici hyperboly se středem S [0; 0], která prochází body: A [5; 3] B [8; -10]
Napište rovnici hyperboly se středem S [0; 0], která prochází body: A [5; 3] B [8; -10] - Parametricky 6400
 Určete úhel přímky, která je určena parametricky x=5+t y=1+3t z=-2t t patři R a roviny, která je určena obecnou rovnicí 2x-y+3z-4=0.
Určete úhel přímky, která je určena parametricky x=5+t y=1+3t z=-2t t patři R a roviny, která je určena obecnou rovnicí 2x-y+3z-4=0.
- Přímka
 Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c.
Napište rovnici přímky rovnoběžné s 9x + 3y = 8, která prochází bodem (-1, -4). Napište ve tvaru ax + by = c. - Střed úsečky
 Body P & Q patří do úsečky AB. Pokud AB = a, AP = 2PQ = 2QB, najděte vzdálenost: mezi bodem A a středem úsečky QB.
Body P & Q patří do úsečky AB. Pokud AB = a, AP = 2PQ = 2QB, najděte vzdálenost: mezi bodem A a středem úsečky QB. - Kružnice 80449
 Najděte rovnici kružnice, jejíž průměr má koncové body (1,-4) a (3,2).
Najděte rovnici kružnice, jejíž průměr má koncové body (1,-4) a (3,2). - Kružnice
 Dokažte, že rovnice k1 a k2 představují kružnice. Napište rovnici přímky, která prochází středy těchto kružnic. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
Dokažte, že rovnice k1 a k2 představují kružnice. Napište rovnici přímky, která prochází středy těchto kružnic. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0 - Trojúhelník KLM
 Dané jsou body K (-3; 2), L (-1; 4), M (3, -4). zjistěte: a) zda je trojúhelník KLM pravoúhlý b) vypočítejte délku těžnice na stranu k c) napište souřadnice vektoru LM d) napište smernicový tvar strany KM e) napište smernicový tvar osy strany KM
Dané jsou body K (-3; 2), L (-1; 4), M (3, -4). zjistěte: a) zda je trojúhelník KLM pravoúhlý b) vypočítejte délku těžnice na stranu k c) napište souřadnice vektoru LM d) napište smernicový tvar strany KM e) napište smernicový tvar osy strany KM
- 9x^2−4y^2=36 82642
 Napište rovnici tečny hyperboly 9x²−4y²=36 v bodě T =[t1,4].
Napište rovnici tečny hyperboly 9x²−4y²=36 v bodě T =[t1,4]. - Reprezentaci 50311
 Lujza roznáší noviny ve svém okolí. Pokud vykreslíte body (-1, 1), (4, 1), (4, -2) a (-1, -2), napište reprezentaci trasy, kterou ujede v mílích. Kolik kilometrů ujede její trasa?
Lujza roznáší noviny ve svém okolí. Pokud vykreslíte body (-1, 1), (4, 1), (4, -2) a (-1, -2), napište reprezentaci trasy, kterou ujede v mílích. Kolik kilometrů ujede její trasa? - Kulová plocha
 Získejte rovnici kulové plochy se středem na čáře 3x + 2z = 0 = 4x-5y a prochází body (0, -2, -4) a (2, -1,1).
Získejte rovnici kulové plochy se středem na čáře 3x + 2z = 0 = 4x-5y a prochází body (0, -2, -4) a (2, -1,1).
