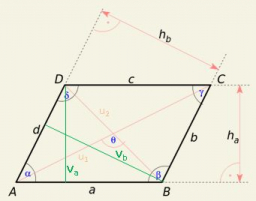
Kosodélník 5
Určete obvod a obsah kosodélníku ABCD, jehož kratší strana AD má délku 5 cm a pata výšky vedené vrcholem D ke straně AB dělí stranu AB na dva úseky délek 3 cm a 4 cm.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Sestrojený čtverce
 Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm². Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB. Vy
Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm². Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB. Vy - Trojúhelníku 4434
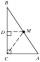 Pata výšky z vrcholu C v trojúhelníku ABC dělí stranu AB v poměru 1:2. Dokažte, že při obvyklém označení délek stran trojúhelníku ABC platí nerovnost 3|a-b| < c.
Pata výšky z vrcholu C v trojúhelníku ABC dělí stranu AB v poměru 1:2. Dokažte, že při obvyklém označení délek stran trojúhelníku ABC platí nerovnost 3|a-b| < c. - Kosodélníku 4285
 Vypočítej obvod kosodélníku, jehož jedna jeho strana má délku 6 cm a výška na tuto stranu má délku 2 cm. Výška na druhou stranu je dlouhá 4 cm.
Vypočítej obvod kosodélníku, jehož jedna jeho strana má délku 6 cm a výška na tuto stranu má délku 2 cm. Výška na druhou stranu je dlouhá 4 cm. - Vypočítej 45
 Vypočítej výšku příslušnou ke straně rovnoběžníku ABCD, má - li strana délku 7,4 cm a obsah rovnoběžníku je 33,3 cm2
Vypočítej výšku příslušnou ke straně rovnoběžníku ABCD, má - li strana délku 7,4 cm a obsah rovnoběžníku je 33,3 cm2
- Pravoúhlý lichoběžník 5
 Pravoúhlý lichoběžník ABCD, jehož rameno AD je kolmé na základny AB a CD, má obsah 15cm čtverečních. Základny mají délky AB=6cm, CD=4cm. Vypočítej délku úhlopříčky AC.
Pravoúhlý lichoběžník ABCD, jehož rameno AD je kolmé na základny AB a CD, má obsah 15cm čtverečních. Základny mají délky AB=6cm, CD=4cm. Vypočítej délku úhlopříčky AC. - Kosodélníku 83302
 Vypočítej výšku kosodélníku ABCD na stranu BC, je-li AB=7cm, BC=5,5cm a výška první strany na AB=4,4cm
Vypočítej výšku kosodélníku ABCD na stranu BC, je-li AB=7cm, BC=5,5cm a výška první strany na AB=4,4cm - Obsah
 Obsah kosodélníku je 32 cm². Jedna jeho strana měří 10 cm. Výška na druhou stranu měří 5 cm. Jaký je obvod tohoto kosodélníku?
Obsah kosodélníku je 32 cm². Jedna jeho strana měří 10 cm. Výška na druhou stranu měří 5 cm. Jaký je obvod tohoto kosodélníku? - Centimetrech 81126
 V pravoúhlém trojúhelníku má přepona délku 24cm. Pata výšky na přeponu ji dělí na dvě části v poměru 2:4. Jakou velikost v cm má výška na přeponu? Vypočítejte v centimetrech obvod tohoto pravoúhlého trojúhelníku.
V pravoúhlém trojúhelníku má přepona délku 24cm. Pata výšky na přeponu ji dělí na dvě části v poměru 2:4. Jakou velikost v cm má výška na přeponu? Vypočítejte v centimetrech obvod tohoto pravoúhlého trojúhelníku. - Rovnoramenném 6183
 V rovnoramenném lichobezniku ABCD je délka základní a=10cm, c=6cm, délka ramene je 4cm. Vypoctej jeho výšku. Výsledek uved zaokruhleny na desetiny
V rovnoramenném lichobezniku ABCD je délka základní a=10cm, c=6cm, délka ramene je 4cm. Vypoctej jeho výšku. Výsledek uved zaokruhleny na desetiny
- Rovnoběžníku 2598
 Vypočítej obvod a obsah rovnoběžníku ABCD, pokud a=72cm va=4,3cm b=6cm
Vypočítej obvod a obsah rovnoběžníku ABCD, pokud a=72cm va=4,3cm b=6cm - Úhlopříčka 5809
 V obdélníku ABCD má strana AB délku 16 cm a úhlopříčka AC délku 20 cm. Vypočítej obvod a obsah obdélníku.
V obdélníku ABCD má strana AB délku 16 cm a úhlopříčka AC délku 20 cm. Vypočítej obvod a obsah obdélníku. - Těžiště 6
 V rovnoramenném trojúhelníku ABC je poměr délek základny AB a výšky na základnu 10:12. Rameno má délku 26 cm. Je-li T těžištěm trojúhelníku ABC, určete obsah trojúhelníku ABT.
V rovnoramenném trojúhelníku ABC je poměr délek základny AB a výšky na základnu 10:12. Rameno má délku 26 cm. Je-li T těžištěm trojúhelníku ABC, určete obsah trojúhelníku ABT. - Trojúhelníku 3147
 V pravoúhlém trojúhelníku ABC má výška na stranu c délku 6 cm. Písmenem D označíme patu výšky. Úsečka AD má délku 8 cm. Vypočítejte obsah trojúhelníku ABC. ( příklad na Monitor 9 )
V pravoúhlém trojúhelníku ABC má výška na stranu c délku 6 cm. Písmenem D označíme patu výšky. Úsečka AD má délku 8 cm. Vypočítejte obsah trojúhelníku ABC. ( příklad na Monitor 9 ) - Čtyřúhelníku 80729
 Čtyřúhelník ABCD má délky stran AB=13cm, CD=3cm, AD=4cm. Úhly ACB a ADC jsou pravé. Vypočítej obvod čtyřúhelníku ABCD.
Čtyřúhelník ABCD má délky stran AB=13cm, CD=3cm, AD=4cm. Úhly ACB a ADC jsou pravé. Vypočítej obvod čtyřúhelníku ABCD.
- Kosočtverec
 Je dán kosočtverec o délky strany a=23 cm. Dotykový bod vepsané kružnice dělí jeho stranu na úseky a1=11 cm a a2=12 cm. Určete poloměr r této kružnice a délky uhlopríček kosočtverce.
Je dán kosočtverec o délky strany a=23 cm. Dotykový bod vepsané kružnice dělí jeho stranu na úseky a1=11 cm a a2=12 cm. Určete poloměr r této kružnice a délky uhlopríček kosočtverce. - Kosodélník
 Kosodélník (rovnoběžník) má delší stranu dlouhou 50 cm. Velikost jeho jedné výšky je 4krát větší než velikost jeho druhé výšky. Vypočítejte v centimetrech délku kratší strany tohoto rovnoběžníku.
Kosodélník (rovnoběžník) má delší stranu dlouhou 50 cm. Velikost jeho jedné výšky je 4krát větší než velikost jeho druhé výšky. Vypočítejte v centimetrech délku kratší strany tohoto rovnoběžníku. - Čtverec
 Vypočítejte stranu čtverce, jehož obsah se rovná obsahu obdélníku, který má délku o 3 cm větší a šířku o 2 cm menší, než je strana čtverce.
Vypočítejte stranu čtverce, jehož obsah se rovná obsahu obdélníku, který má délku o 3 cm větší a šířku o 2 cm menší, než je strana čtverce.
