Příklady na kruh, kružnice - strana 37 z 46
Počet nalezených příkladů: 918
- Rovnoběžné tětivy
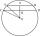 V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv.
V kružnici s r = 26 cm jsou narýsované 2 rovnoběžné tětivy. Jedna tětiva má délku t1 = 48 cm a druhá má délku t2 = 20cm, přičemž střed leží mezi nimi. Vypočítejte vzdálenost dvou tětiv. - Tětiva
 Jakou délku x má tětiva kružnice o průměru 120 km, pokud je vzdálena od středu kružnice 14 km?
Jakou délku x má tětiva kružnice o průměru 120 km, pokud je vzdálena od středu kružnice 14 km? - Tetiva
 Bod na kružnici je krajním bodem průměru a tětivy velikosti poloměru. Jaký úhel svírá průměr s tětivou?
Bod na kružnici je krajním bodem průměru a tětivy velikosti poloměru. Jaký úhel svírá průměr s tětivou? - Šestiúhelník 5
 Vzdálenost rovnoběžných stran pravidelného šestiúhelníku je 53 cm. Vypočítejte velikost poloměru kružnice opsané šestiúhelníku.
Vzdálenost rovnoběžných stran pravidelného šestiúhelníku je 53 cm. Vypočítejte velikost poloměru kružnice opsané šestiúhelníku. - Pravidelný n-uhelnik
 Který pravidelný n-uhelnik má polomer opsane kružnice r=10 cm, a polomer vepsané kružnice p=9,962 cm?
Který pravidelný n-uhelnik má polomer opsane kružnice r=10 cm, a polomer vepsané kružnice p=9,962 cm? - Je dána 4
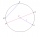 Je dána kružnice o poloměru 10 cm a její tětiva, která má délku 12 cm. Vypočtěte velikost středového úhlu, který této tětivě přísluší.
Je dána kružnice o poloměru 10 cm a její tětiva, která má délku 12 cm. Vypočtěte velikost středového úhlu, který této tětivě přísluší. - Vepsán v kruhu
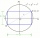 Jaký je obvod obdélníku, který je vepsán v kruhu, jehož průměr je 5 dm?
Jaký je obvod obdélníku, který je vepsán v kruhu, jehož průměr je 5 dm? - 10 dílů
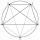 Jak rozdělit kruh na 10 dílů (geometricky)?
Jak rozdělit kruh na 10 dílů (geometricky)? - Sestrojte kosočtverec
 Sestrojte kosočtverec ABCD, jestliže je dána délka úhlopříčky | AC | = 8cm, poloměr vepsané kružnice r = 1,5cm
Sestrojte kosočtverec ABCD, jestliže je dána délka úhlopříčky | AC | = 8cm, poloměr vepsané kružnice r = 1,5cm - Dve tětivy
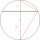 Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm.
Vypočítejte délku tětivy AB a k ní kolmé tětivy BC, pokud tětiva AB je od středu kružnice k vzdálená 4 cm a tětiva BC má vzdálenost 8 cm. - Potrubí
 O kolik procent se změnil (zmenšil) obsah průřezu plechového potrubí, jehož kruhový tvar při stejném obvodu změnili na čtvereční?
O kolik procent se změnil (zmenšil) obsah průřezu plechového potrubí, jehož kruhový tvar při stejném obvodu změnili na čtvereční? - Druhá strana a obsah obdélníku
 Poloměr kružnice opsané obdélníku je 5 cm, jedna strana obdélníku má délku 6 cm. Vypočítej délku druhé strany a obsah obdélníku.
Poloměr kružnice opsané obdélníku je 5 cm, jedna strana obdélníku má délku 6 cm. Vypočítej délku druhé strany a obsah obdélníku. - Nepravidelný čtyřúhelník
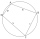 Daný je 4-úhelník ABCD vepsaný do kružnice, přičemž úhlopříčka AC je průměr kružnice. Vzdálenost bodu B od průměru je 15 cm, vzdálenost bodu D od průměru je 18 cm. Vypočítejte poloměr kružnice a obvod 4-úhelníku ABCD.
Daný je 4-úhelník ABCD vepsaný do kružnice, přičemž úhlopříčka AC je průměr kružnice. Vzdálenost bodu B od průměru je 15 cm, vzdálenost bodu D od průměru je 18 cm. Vypočítejte poloměr kružnice a obvod 4-úhelníku ABCD. - V kružnici
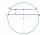 V kružnici o poloměru 8,5 cm jsou sestrojeny dvě rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost tětiv v kružnici.
V kružnici o poloměru 8,5 cm jsou sestrojeny dvě rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost tětiv v kružnici. - Šestihran
 Pravidelný šestihran (6 úhelník) se stěnou 6 cm je otočen o 60 ° podél přímky procházející její nejdelší úhlopříčce. Jaký je objem takto vytvořeného tělesa?
Pravidelný šestihran (6 úhelník) se stěnou 6 cm je otočen o 60 ° podél přímky procházející její nejdelší úhlopříčce. Jaký je objem takto vytvořeného tělesa? - Dvanáctiúhelník
 Vypočti obsah pravidelného dvanáctiúhelníku jestliže poloměr kružnice opsané je 5 cm.
Vypočti obsah pravidelného dvanáctiúhelníku jestliže poloměr kružnice opsané je 5 cm. - Hodiny
 Velké ručičkové hodiny v jistý náhodný okamžik zastali. Jaká je pravděpodobnost, že: a) malá ručička ukazovala čas mezi 1:00 až 3:00? b) velká ručička byla ve stejném území jako malá ručička v roli a)? c) hodiny právě ukazovaly čas mezi 21:00 a 22:30?
Velké ručičkové hodiny v jistý náhodný okamžik zastali. Jaká je pravděpodobnost, že: a) malá ručička ukazovala čas mezi 1:00 až 3:00? b) velká ručička byla ve stejném území jako malá ručička v roli a)? c) hodiny právě ukazovaly čas mezi 21:00 a 22:30? - Z8 – I – 1 MO 2019
 Sestrojte kosočtverec ABCD tak, aby jeho úhlopříčka BD měla velikost 8 cm a vzdálenost vrcholu B od přímky AD byla 5 cm. Určete všechny možnosti. Jaká je délka strany kosočtverce?
Sestrojte kosočtverec ABCD tak, aby jeho úhlopříčka BD měla velikost 8 cm a vzdálenost vrcholu B od přímky AD byla 5 cm. Určete všechny možnosti. Jaká je délka strany kosočtverce? - Minutová ručička
 Jakou dráhu popíše hrot minutové ručičky hodin dlouhé 6cm za 20 minut pokud víme, že počáteční poloha ručičky s konečnou svírají navzájem úhel 120°?
Jakou dráhu popíše hrot minutové ručičky hodin dlouhé 6cm za 20 minut pokud víme, že počáteční poloha ručičky s konečnou svírají navzájem úhel 120°? - Rovnice kružnice
 Najděte rovnici kružnice, která se dotýká osy y ve vzdálenosti 4 od počátku a vysekne tětivu délky 6 na ose x.
Najděte rovnici kružnice, která se dotýká osy y ve vzdálenosti 4 od počátku a vysekne tětivu délky 6 na ose x.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
