Příklady na kruh, kružnice - strana 43 z 46
Počet nalezených příkladů: 918
- Plátky sýra
 Myši vyhlodaly do plátku sýra kruhové díry. Sýr má tvar kruhové výseče o poloměru 20 cm a úhlu 90 stupňů. Jakou část sýra v procentech myši sežraly, pokud vyhlodaly 20 děr o průměru 2 cm?
Myši vyhlodaly do plátku sýra kruhové díry. Sýr má tvar kruhové výseče o poloměru 20 cm a úhlu 90 stupňů. Jakou část sýra v procentech myši sežraly, pokud vyhlodaly 20 děr o průměru 2 cm? - Mezikruží
 Čtverci o obsahu 16 centimetrů čtverečních je vepsaná kružnice k1 a opsána kružnice k2. Vypočtěte obsah mezikruží, které kružnice k1, k2 ohraničují.
Čtverci o obsahu 16 centimetrů čtverečních je vepsaná kružnice k1 a opsána kružnice k2. Vypočtěte obsah mezikruží, které kružnice k1, k2 ohraničují. - Kruhový výsek
 Kruhový výsek má obvod 73,3 km a obsah 1099,56 km². Vypočítej poloměr příslušné kružnice a velikost středového úhlu výseku.
Kruhový výsek má obvod 73,3 km a obsah 1099,56 km². Vypočítej poloměr příslušné kružnice a velikost středového úhlu výseku. - Válec horizontálně
 Kolik nafty je ve vodorovné nádrži ve tvaru válce o délce 10m, když šířka hladiny je 1m a hladina je 0,2m pod horní stranou válce?
Kolik nafty je ve vodorovné nádrži ve tvaru válce o délce 10m, když šířka hladiny je 1m a hladina je 0,2m pod horní stranou válce? - Čtverci
 Čtverci o straně a=1 je vepsaná a opsaná kružnice. Určete obsah mezikruží.
Čtverci o straně a=1 je vepsaná a opsaná kružnice. Určete obsah mezikruží. - Soustředna kružnice
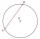 V kružnici s průměrem 16 cm je sestrojena tětiva délky 8 cm. Vypočtěte poloměr soustředné kružnice, která se dotýká tětivy.
V kružnici s průměrem 16 cm je sestrojena tětiva délky 8 cm. Vypočtěte poloměr soustředné kružnice, která se dotýká tětivy. - Kruhový výsek
 Jakou plochu kruhu zabírají květiny vysázeny v kruhovém výseku s poloměrem 2 m a středovým úhlem 45°?
Jakou plochu kruhu zabírají květiny vysázeny v kruhovém výseku s poloměrem 2 m a středovým úhlem 45°? - Mezikruží
 Na obrázku jsou 2 soustředné kružnice. Tětiva větší kružnice s délkou 10 cm je tečnou menší kružnice. Jaký obsah má mezikruží?
Na obrázku jsou 2 soustředné kružnice. Tětiva větší kružnice s délkou 10 cm je tečnou menší kružnice. Jaký obsah má mezikruží? - Oblouk
 Délka kružnice je 41 a délka oblouku na této kružnici je 17. Jaká je velikost úhlu který vytíná na kružnici tento oblouk?
Délka kružnice je 41 a délka oblouku na této kružnici je 17. Jaká je velikost úhlu který vytíná na kružnici tento oblouk? - Postřikování - závlaha
 Jakou plochu trávy může postřikovat automatický postřikovač, je-li nastaven na postřikování s úhlem 120° a voda dostříkne do vzdálenosti nejvýše 5 metrů?
Jakou plochu trávy může postřikovat automatický postřikovač, je-li nastaven na postřikování s úhlem 120° a voda dostříkne do vzdálenosti nejvýše 5 metrů? - Výseč II
 délka oblouku = 17cm obsah kruhové výseče = 55 cm² úhel kruhové výseče = ? poloměr kruhové výseče = ?
délka oblouku = 17cm obsah kruhové výseče = 55 cm² úhel kruhové výseče = ? poloměr kruhové výseče = ? - Oblouk
 Kružnicových oblouk příslušející úhlu 291° je dlouhý 19 dm. Jaká je délka celé kružnice?
Kružnicových oblouk příslušející úhlu 291° je dlouhý 19 dm. Jaká je délka celé kružnice? - V rovnostranném
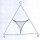 V rovnostranném trojúhelníku o straně 2cm jsou zakresleny oblouky tří kružnic se středy ve vrcholech trojúhelníku a poloměry 1cm. Vypočítej obsah vyšrafované části - útvaru ktorý tvorí rozdíl mezi plochou trojuholníka a kruhovými výsekmi.
V rovnostranném trojúhelníku o straně 2cm jsou zakresleny oblouky tří kružnic se středy ve vrcholech trojúhelníku a poloměry 1cm. Vypočítej obsah vyšrafované části - útvaru ktorý tvorí rozdíl mezi plochou trojuholníka a kruhovými výsekmi. - Je dána 5
 Je dána kružnice, do které je vepsán čtverec. Menší čtverec je vepsán do kruhové úseče tvořené stranou čtverce a obloukem dané kružnice. Jaký je poměr ploch velkého a malého čtverce?
Je dána kružnice, do které je vepsán čtverec. Menší čtverec je vepsán do kruhové úseče tvořené stranou čtverce a obloukem dané kružnice. Jaký je poměr ploch velkého a malého čtverce? - Výsek a kužel
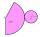 Vypočítejte objem rotačního kužele, jehož pláštěm je kruhová výseč s poloměrem 13 cm a středovým úhlem 47 stupňů.
Vypočítejte objem rotačního kužele, jehož pláštěm je kruhová výseč s poloměrem 13 cm a středovým úhlem 47 stupňů. - Vepsány čtyřúhelník
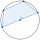 Do kružnice je vepsán čtyřúhelník tak, že jeho vrcholy dělí kružnici 1:2:3:4. Vypočítejte velikosti jeho vnitřních úhlů.
Do kružnice je vepsán čtyřúhelník tak, že jeho vrcholy dělí kružnici 1:2:3:4. Vypočítejte velikosti jeho vnitřních úhlů. - Kruh-výseč
 Rovnostrannému trojúhelníku o straně 17 je vepsána kruhová výseč, jejíž střed je v jednom z vrcholů trojúhelníku a oblouk se dotýká protější strany. Vypočtěte: a) délku oblouku výseče b) poměr obvodu výseče v ku obvodu trojúhelníka
Rovnostrannému trojúhelníku o straně 17 je vepsána kruhová výseč, jejíž střed je v jednom z vrcholů trojúhelníku a oblouk se dotýká protější strany. Vypočtěte: a) délku oblouku výseče b) poměr obvodu výseče v ku obvodu trojúhelníka - Rameno kolotoče
 Na dětském kolotoči ve tvaru kružnice je rovnoměrně rozmístěno 12 sedaček. Jak dlouhé je rameno kolotoče (spojující střed kolotoče se sedačkou), pokud vzdálenost mezi dvěma sedačkami je 1,5m.
Na dětském kolotoči ve tvaru kružnice je rovnoměrně rozmístěno 12 sedaček. Jak dlouhé je rameno kolotoče (spojující střed kolotoče se sedačkou), pokud vzdálenost mezi dvěma sedačkami je 1,5m. - Odmocnina - tětiva
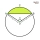 Tětiva o délce t = r krát druhá odmocnina dva rozděluje, kruh o poloměru r na dva kruhové odseky. V jakém poměru jsou obsahy těchto odseků?
Tětiva o délce t = r krát druhá odmocnina dva rozděluje, kruh o poloměru r na dva kruhové odseky. V jakém poměru jsou obsahy těchto odseků? - Oblouk 7
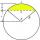 Rozpětí oblouku je 247 cm, výška oblouku je 21,5 cm . Jaký je průměr kruhu ?
Rozpětí oblouku je 247 cm, výška oblouku je 21,5 cm . Jaký je průměr kruhu ?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
