Kombi-troj
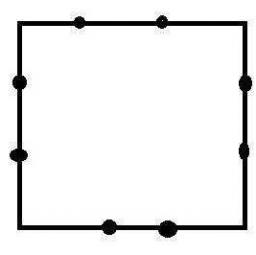
Na každej strane štvorca je vyznačených 3 rôznych bodov, mimo vrcholov štvorca. Koľko trojuholníkov možno zostrojiť z tejto množiny bodov, ak každý vrchol trojuholníka má ležať na inej strane štvorca?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
kombinatorikaaritmetikaplanimetriazákladné operácie a pojmyÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Trojuholníky
Daný je štvorec ABCD a na každej jeho strane je zvolených n jej vnútorných bodov. Určte počet všetkých trojuholníkov, ktorých vrcholy X, Y, Z ležia v týchto bodoch a na rôznych stranách štvorca. - N bodov na strane
Daný je rovnostranny trojuholník A, B, C na každej jeho vnútornej strane N=13 bodov. Určite počet všetkých trojuholníkov, ktorých vrcholy ležia v daných bodoch na rôznych stranách. - Počet trojuholníkov
Je daný štvorec ABCD a na každej jeho strane 6 vnútorných bodov. Určte počet všetkých trojuholníkov s vrcholmi v týchto bodoch. - Pravdepodobnosť 81637
Z vrcholov pravidelného sedemuholníka vyberieme náhodne trojicu rôznych bodov a spojíme ich úsečkami. Pravdepodobnosť, že výsledný trojuholník bude rovnoramenný, je rovná: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - Kruh - úsek
Rovnostrannému trojuholníku o strane 19 je vpísaná kruhový výsek, ktorého stred je v jednom z vrcholov trojuholníka a oblúk sa dotýka protiľahlej strany. Vypočítajte: a) dĺžku oblúka výseku b) pomer obvodu výseku ku obvodu trojuholníka - Rovnoramenný trojuholník 7
Daných je 6 úsečiek s dĺžkami 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, 9 cm, z každej dĺžky po dve. Koľko rovnoramenných trojuholníkov sa z nich dá zostrojiť? Vypíš všetky možnosti. - Vzdialenosť 80164
Je daný štvorec ABCD 4,2 cm. Zostroj množinu všetkých bodov, ktoré majú od niektorého z vrcholov vzdialenosť menšiu alebo rovnú 2 cm a zároveň leží vo vnútri tohto štvorca . Uveď v percentách, akú veľkú časť štvorca táto oblasť zaberá.
