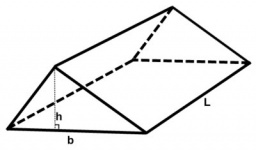
Určí objem
Určí objem a povrch trojbokeho hranola s podstavou pravouhlého trojuholníka, ktorého sieť je 4 cm 3 cm (odvesny) a deväť centimetrov (výška hranola).
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikastereometriaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Trojboký hranol
Vypočítaj povrch a objem trojbokého hranola s podstavou tvaru pravouhlého trojuholníka, ak a=3 cm, b=4 cm, c=5 cm a výška hranola v=12 cm. - Hranol 6
Urč objem a povrch hranola s podstavou pravouhlého trojuholníka ak odvesny sú: a je 1,2 cm. b je 2 cm. a výška telesa je 0,3 dm. - Aký je
Aký je objem trojbokého hranola s podstavou pravouhlého trojuholníka s odvesnami 6 dm a 8 dm a preponou 10 dm a výška hranola je 40 dm? - Vypočítaj 13
Vypočítaj koľko zaplatíme za papier na oblepenie krabičky tvaru trojbokého hranola s podstavou pravouhlého trojuholníka ak odvesny merajú 12 cm a 1,6 decimetra prepona meria 200 milimetrov, krabička je vysoká 27 centimetrov. Za jeden decimeter štvorcový p - Trojuholník - podstava
Vypočítajte objem a povrch trojbokého kolmého hranola s podstavou pravouhlého trojuholníka, pokiaľ dĺžky odvesny a základne sú 7,2 cm a 4,7 cm, výška hranola je 24 cm. - Hranol s podstavou
Aká je výška hranola s podstavou pravouhlého trojuholníka s odvesnami osem centimetrov a desať centimetrov a s objemom 0,098 decimetrov kubických - Trojuholník - hranol
A = 3 cm b = 4 cm výška hranola v=10 cm Vypočítajte objem trojbokého hranola so základňou pravouhlého trojuholníka - odvesne a, b.
