Špeh a opilec

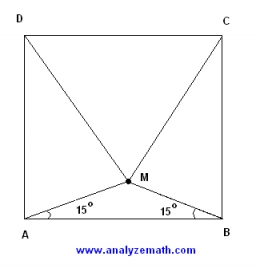
Po dlhom večeri vo vnútri salónika v tvare štvorca ABCD leží opitý kupec E tak, že trojuholník DEC je rovnostranný. Na hrane BC
leží špeh F, pričom |EB|=|EF|. Aká je veľkosť uhla CEF?

Správna odpoveď:

x =  45 °

Postup správneho riešenia:

$$\begin{gathered} a=1 \\ h=\sqrt{3}/2\cdot a=\sqrt{3}/2\cdot 1\doteq 0,866 \\ b=a-h=1-0,866\doteq 0,134 \\ \mathrm{tg}y=b:a/2 \\ y=\frac{180°}{\pi }\cdot \mathrm{arctg}(b/(a/2))=\frac{180°}{\pi }\cdot \mathrm{arctg}(0,134/(1/2))=15{}^{\circ } \\ x=90-60/2-y=90-60/2-15=45^{\circ } \end{gathered}$$

Skúsiť iný príklad