Obdĺžnik - kto má pravdu
Obdĺžnik je rozdelený na 7 políčok. Na každé políčko sa má napísať práve jedno z čísel 1, 2 a 3.
Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto z nich má pravdu.
Výsledok
Mirek tvrdia, že to možno vykonať tak, aby súčet dvoch vedľa seba napísaných čísel bol zakaždým iný. Zuzka naopak tvrdia, že to možné nie je. Rozhodnite, kto z nich má pravdu.
Výsledok

Zobrazujem 2 komentáre:
Peter5
Nápoveda. Zistite, ktoré rôzne súčty možno získať.
Možné riešenie. Všetky možné dvojice, ktoré možno z daných čísel zložiť, sú (1,1); (1,2), (2,1); (1,3), (2,2), (3,1); (2,3), (3,2); (3,3).
Tieto možnosti dávajú 5 rôznych súčtov, a to 2, 3, 4, 5, 6 (dvojice s rôznymi súčtami sú oddelené bodkočiarkami). Na uvedenom obrázku však potrebujeme 6 dvojíc s rôznymi súčty, pravdu má teda Zuzka.
Poznámky.
a) Na určenie možných súčtov netreba vypisovať všetky prípustné dvojice:
najmenší súčet odpovedá 1 + 1 = 2, najväčší je 3 + 3 = 6. Odtiaľ vyplýva, že možných súčtov nie je viac ako 5, čo je menej ako požadovaných 6.
b) Riešenie úlohy pomocou všetkých možných vyplnenie tabuľky a kontrolou takto získaných súčtov je extrémne prácne.
Možné riešenie. Všetky možné dvojice, ktoré možno z daných čísel zložiť, sú (1,1); (1,2), (2,1); (1,3), (2,2), (3,1); (2,3), (3,2); (3,3).
Tieto možnosti dávajú 5 rôznych súčtov, a to 2, 3, 4, 5, 6 (dvojice s rôznymi súčtami sú oddelené bodkočiarkami). Na uvedenom obrázku však potrebujeme 6 dvojíc s rôznymi súčty, pravdu má teda Zuzka.
Poznámky.
a) Na určenie možných súčtov netreba vypisovať všetky prípustné dvojice:
najmenší súčet odpovedá 1 + 1 = 2, najväčší je 3 + 3 = 6. Odtiaľ vyplýva, že možných súčtov nie je viac ako 5, čo je menej ako požadovaných 6.
b) Riešenie úlohy pomocou všetkých možných vyplnenie tabuľky a kontrolou takto získaných súčtov je extrémne prácne.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Z9–I–4 MO 2017
 Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 sa chystali na cestu vlakom s tromi vagónmi. Chceli sa rozsadiť tak, aby v každom vagóne sedeli tri čísla a najväčšie z každej trojice bolo rovné súčtu zvyšných dvoch. Sprievodca tvrdil, že to nie je problém, a snažil sa č
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 sa chystali na cestu vlakom s tromi vagónmi. Chceli sa rozsadiť tak, aby v každom vagóne sedeli tri čísla a najväčšie z každej trojice bolo rovné súčtu zvyšných dvoch. Sprievodca tvrdil, že to nie je problém, a snažil sa č - Dávidovo číslo
 Jana a David trénujú sčítanie desatinných čísel tak, ze každý z nich napíše jedno číslo, a tieto dve čísla potom spočítajú. Posledný príklad im vyšiel 11,11. Dávidovo číslo malo pred desatinnou čiarkou rovnaký počet číslic ako za ňou, Janino číslo tiež. D
Jana a David trénujú sčítanie desatinných čísel tak, ze každý z nich napíše jedno číslo, a tieto dve čísla potom spočítajú. Posledný príklad im vyšiel 11,11. Dávidovo číslo malo pred desatinnou čiarkou rovnaký počet číslic ako za ňou, Janino číslo tiež. D - 7 kníh
 Koľkými spôsobmi možno uložiť na poličke 7 kníh, ak je medzi nimi jeden trojdielny román, ktorý má byť uložený vedľa seba?
Koľkými spôsobmi možno uložiť na poličke 7 kníh, ak je medzi nimi jeden trojdielny román, ktorý má byť uložený vedľa seba? - Deti
 Stretnú sa dvaja priatelia a ako správni chlapi zájdu spolu na pivo. Po prebratí najdôležitejších tém (politika, ženy, futbal...), sa jeden pýta: - A koľko máš vlastne detí? - Mám 3 deti. - A koľko majú rokov? Priateľovi sa už nechce odpovedať na priamu o
Stretnú sa dvaja priatelia a ako správni chlapi zájdu spolu na pivo. Po prebratí najdôležitejších tém (politika, ženy, futbal...), sa jeden pýta: - A koľko máš vlastne detí? - Mám 3 deti. - A koľko majú rokov? Priateľovi sa už nechce odpovedať na priamu o
- Na papieri
 Na papieri bolo napísaných niekoľko kladných celých čísel. Miška si pamätala iba to, že každé číslo bolo polovicou súčtu všetkých ostatných čísel. Koľko čísel mohlo byť napísaných na papieri?
Na papieri bolo napísaných niekoľko kladných celých čísel. Miška si pamätala iba to, že každé číslo bolo polovicou súčtu všetkých ostatných čísel. Koľko čísel mohlo byť napísaných na papieri? - MO Z6-1-3 2017 šachovnica
 Veronika má klasickú šachovnicu s 8×8 políčkami. Riadky sú označené ciframi 1 až 8, stĺpce písmenami A až H. Veronika položila na políčko B1 jazdca, s ktorým možno pohybovať iba tak ako v šachu. 1. Je možné premiestniť jazdca štyrmi ťahmi na políčko H1? 2
Veronika má klasickú šachovnicu s 8×8 políčkami. Riadky sú označené ciframi 1 až 8, stĺpce písmenami A až H. Veronika položila na políčko B1 jazdca, s ktorým možno pohybovať iba tak ako v šachu. 1. Je možné premiestniť jazdca štyrmi ťahmi na políčko H1? 2 - Palko
 Palko má 5 kartičiek s číslicami 0, 1, 6, 7, 9. Kolko nepárnych trojciferných čísel z nich môže utvoriť?
Palko má 5 kartičiek s číslicami 0, 1, 6, 7, 9. Kolko nepárnych trojciferných čísel z nich môže utvoriť? - Z7–I–6, výstava mačiek
 Na výstave dlhosrstých mačiek sa zišlo celkom desať vystavujúcich. Vystavovalo sa v obdĺžnikovej miestnosti, v ktorej boli dva rady stolov ako na obrázku. Mačky boli označené navzájom rôznymi číslami v rozmedzí 1 až 10 a na každom stole sedela jedna mačka
Na výstave dlhosrstých mačiek sa zišlo celkom desať vystavujúcich. Vystavovalo sa v obdĺžnikovej miestnosti, v ktorej boli dva rady stolov ako na obrázku. Mačky boli označené navzájom rôznymi číslami v rozmedzí 1 až 10 a na každom stole sedela jedna mačka - Dve skupiny
 Skupina 10 dievčat sa má rozdeliť na dve skupiny tak, aby v každej boli najmenej 4 dievčatá. Koľkými spôsobmi to možno vykonať?
Skupina 10 dievčat sa má rozdeliť na dve skupiny tak, aby v každej boli najmenej 4 dievčatá. Koľkými spôsobmi to možno vykonať?
- Z pásu
 Z pásu oceľového plechu so šírkou 10 cm a dĺžkou 2 m sú vystrihnuté kovové podložky s priemerom 80 mm. Vypočítajte odpad materiálu v percentách, ak pri styku dvoch susedných kruhov nedochádza k žiadnej strate materiálu.
Z pásu oceľového plechu so šírkou 10 cm a dĺžkou 2 m sú vystrihnuté kovové podložky s priemerom 80 mm. Vypočítajte odpad materiálu v percentách, ak pri styku dvoch susedných kruhov nedochádza k žiadnej strate materiálu. - Pán Cuketa
 Pán Cuketa mal obdĺžnikovú záhradu, ktorej obvod bol 28 metrov. Obsah celej záhrady vyplnili práve štyri štvorcové záhony, ktorých rozmery v metroch boli vyjadrené celými číslami. Určite aké rozmery mohla mať záhrada. Nájdite všetky možnosti a zapíšte n a
Pán Cuketa mal obdĺžnikovú záhradu, ktorej obvod bol 28 metrov. Obsah celej záhrady vyplnili práve štyri štvorcové záhony, ktorých rozmery v metroch boli vyjadrené celými číslami. Určite aké rozmery mohla mať záhrada. Nájdite všetky možnosti a zapíšte n a - Nikola
 Nikola mala v zošite napísané jedno trojciferne a jedno dvojciferné číslo. Každé z týchto čísel bolo tvorené navzájom rôznymi číslicami. Rozdiel Nikolinych čísel bol 976. Aký bol ich súčet?
Nikola mala v zošite napísané jedno trojciferne a jedno dvojciferné číslo. Každé z týchto čísel bolo tvorené navzájom rôznymi číslicami. Rozdiel Nikolinych čísel bol 976. Aký bol ich súčet? - MO C-I-1 2019
 Nájdite všetky štvorciferné čísla abcd s ciferným súčtom 12 také, že ab-cd=1
Nájdite všetky štvorciferné čísla abcd s ciferným súčtom 12 také, že ab-cd=1 - MO Z8-I-1 2018
 Fero a Dávid sa denne stretávajú vo výťahu. Raz ráno zistili, že keď vynásobia svoje súčasné veky, dostanú 238. Keby to isté urobili za štyri roky, bol by tento súčin 378. Určte súčet súčasných vekov Fera a Dávida.
Fero a Dávid sa denne stretávajú vo výťahu. Raz ráno zistili, že keď vynásobia svoje súčasné veky, dostanú 238. Keby to isté urobili za štyri roky, bol by tento súčin 378. Určte súčet súčasných vekov Fera a Dávida.
- Muž mal
 Muž mal 4 mince, niektoré dvojdolárovky, niektoré jedno-dolárovky. Mince mali na jednej strane číslo, na druhej len obrázok. Muž si ich hodil a súčet čísel na horných stranách mincí bol 1. Pravdepodobnosť, že nastane táto situácia, bola 1/8. Aká bola v to
Muž mal 4 mince, niektoré dvojdolárovky, niektoré jedno-dolárovky. Mince mali na jednej strane číslo, na druhej len obrázok. Muž si ich hodil a súčet čísel na horných stranách mincí bol 1. Pravdepodobnosť, že nastane táto situácia, bola 1/8. Aká bola v to - Fourland
 V krajine Fourland majú iba štyri písmena F, O, U, R a každé slovo má práve štyri písmena. V žiadnom slove sa nesmie opakovať ani jedno písmeno. Napíš všetky slová, ktoré sa dajú u nich napísať.
V krajine Fourland majú iba štyri písmena F, O, U, R a každé slovo má práve štyri písmena. V žiadnom slove sa nesmie opakovať ani jedno písmeno. Napíš všetky slová, ktoré sa dajú u nich napísať. - MO Z6–I–3 2018
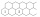 Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude
Na obrázku sú naznačené dva rady šesťuholníkových políčok, ktoré doprava pokračujú bez obmedzenia. Do každého políčka doplňte jedno kladné celé číslo tak, aby súčin čísel v ľubovoľných troch navzájom susediacich políčkach bol 2018. Určte číslo, ktoré bude
