Čtyřúhelniku.
Jak velké jsou úhly čtyřúhelniku, jsou-li v poměru 8:9:10:13?
Správná odpověď:
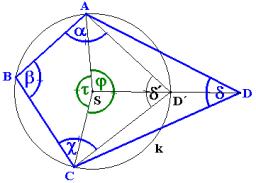
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - V obecném
 V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů.
V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů. - Vzdálenost 71874
 Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla.
Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla. - Na kružnici
 Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC.
Na kružnici o poloměru 10 cm a se středem S jsou dány body A, B, C tak, že středový úhel ASB má 60 stupňů a středový úhel ASC má 90 stupňů. Určete délku oblouku kružnice a velikost posunutí AB a AC.
- Výslednice 3
 Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°.
Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°. - Úhly šestiúhelníku
 Vypočítejte vnitřní úhly šestiúhelníku, jestliže velikosti úhlů tvoří aritmetickou posloupnost a nejmenší úhel má velikost 70°.
Vypočítejte vnitřní úhly šestiúhelníku, jestliže velikosti úhlů tvoří aritmetickou posloupnost a nejmenší úhel má velikost 70°. - Vygumovala 33173
 Jaro měl v sešitě zapsané 4 úhly, jejichž součtem byl přímý úhel. Malá sestra mu jeden úhel vygumovala. Urč jeho velikost, pokud v sešitě zůstane napsáno zbývající úhly: 12°34, 34°56, 56°9.
Jaro měl v sešitě zapsané 4 úhly, jejichž součtem byl přímý úhel. Malá sestra mu jeden úhel vygumovala. Urč jeho velikost, pokud v sešitě zůstane napsáno zbývající úhly: 12°34, 34°56, 56°9. - Motorový člun
 Motorový člun se pohybuje vzhledem k vodě stálou rychlostí 13 m/s. Rychlost vodního proudu v řece je 5 m/s a) Pod jakým úhlem vzhledem k vodnímu proudu musí člun plout, aby se stále pohyboval kolmo ke břehům řeky? b) Jak velkou rychlostí se přibližuje člu
Motorový člun se pohybuje vzhledem k vodě stálou rychlostí 13 m/s. Rychlost vodního proudu v řece je 5 m/s a) Pod jakým úhlem vzhledem k vodnímu proudu musí člun plout, aby se stále pohyboval kolmo ke břehům řeky? b) Jak velkou rychlostí se přibližuje člu - Mnohoúhelník - hexagon
 V šestistranném polygonu - mnohoúhelníku platí - první dva úhly jsou stejné, třetí úhel je dvojnásobný (stejných úhlů), dva další úhly jsou trojnásobkem stejného úhlu, zatímco poslední úhel je pravý úhel. Najděte hodnotu každého úhlu.
V šestistranném polygonu - mnohoúhelníku platí - první dva úhly jsou stejné, třetí úhel je dvojnásobný (stejných úhlů), dva další úhly jsou trojnásobkem stejného úhlu, zatímco poslední úhel je pravý úhel. Najděte hodnotu každého úhlu.
- Výslednice sil
 Vypočtěte matematicky a graficky výslednici soustavy tří sil se společným působištěm, jestliže: F1 = 50kN α1 = 30° F2 = 40kN α2 = 45° F3 = 40kN α3 = 25°
Vypočtěte matematicky a graficky výslednici soustavy tří sil se společným působištěm, jestliže: F1 = 50kN α1 = 30° F2 = 40kN α2 = 45° F3 = 40kN α3 = 25° - Osmistěn
 Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také se
Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také se - Tři síly - vektory
 Tři síly, jejichž velikosti jsou v poměru 9:10:17, působí v rovině v jednom bodě tak, že jsou v rovnováze. Určete velikosti úhlů, které svírají každé dvě síly
Tři síly, jejichž velikosti jsou v poměru 9:10:17, působí v rovině v jednom bodě tak, že jsou v rovnováze. Určete velikosti úhlů, které svírají každé dvě síly - Vektorový součet sil
 Síly o velikostech F1 = 42N a F2 = 35N působí ve společném bodě a svírají úhel o velikosti 77°12´. Jak veliká je jejich výslednice?
Síly o velikostech F1 = 42N a F2 = 35N působí ve společném bodě a svírají úhel o velikosti 77°12´. Jak veliká je jejich výslednice? - Odmocnin 3871
 Čemu se rovná součet pátých odmocnin z čísla 243.
Čemu se rovná součet pátých odmocnin z čísla 243.
- Součet a rozdíl úhlů
 Vypočtěte součet a rozdíl úhlů alfa a beta. Alfa=60°30' ,beta=29°35'.
Vypočtěte součet a rozdíl úhlů alfa a beta. Alfa=60°30' ,beta=29°35'. - Úhly
 Zjisti zda mohou být uvedené hodnoty velikostmi vnitřních úhlů nějakého trojuhelníku: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3'
Zjisti zda mohou být uvedené hodnoty velikostmi vnitřních úhlů nějakého trojuhelníku: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3' - Dvě síly
 Dvě síly s velikostí 25 a 30 Newtonův působí na objekt v úhlech 10° a 100°. Najděte směr a velikost výsledné síly. Zaokrouhlete na dvě desetinná místa mezivýpočty a konečnou odpověď.
Dvě síly s velikostí 25 a 30 Newtonův působí na objekt v úhlech 10° a 100°. Najděte směr a velikost výsledné síly. Zaokrouhlete na dvě desetinná místa mezivýpočty a konečnou odpověď.
