Planimetrie - slovní úlohy a příklady - strana 141 z 177
Počet nalezených příkladů: 3525
- Slneční lúče
 Devíti metrový topol vrhá stín 16,2m. Jak dlouhý stín vrhá ve stejnou dobu Pepík, jestliže je vysoký 1,4m?
Devíti metrový topol vrhá stín 16,2m. Jak dlouhý stín vrhá ve stejnou dobu Pepík, jestliže je vysoký 1,4m? - Trojúhelník P2
 Může mít trojúhelník dva pravé úhly?
Může mít trojúhelník dva pravé úhly? - Narysuj
 Narysuj lichoběžník, pokud b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Postup, diskuse, náčrt, rozbor, konstrukce)
Narysuj lichoběžník, pokud b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Postup, diskuse, náčrt, rozbor, konstrukce) - Výška stromu
 Člověk vysoký 1,65m vrhá stín dluhy 1,25m. Jak vysoký je strom jehož stín je dluhy 2,58 m?
Člověk vysoký 1,65m vrhá stín dluhy 1,25m. Jak vysoký je strom jehož stín je dluhy 2,58 m? - Pravděpodobnost různostranného trojúhelníku
 Máme čísla 4, 6, 8, 10, 12. Jaká je pravděpodobnost, že při náhodně vybrané trojici to budou délky stran různostranného trojúhelníku?
Máme čísla 4, 6, 8, 10, 12. Jaká je pravděpodobnost, že při náhodně vybrané trojici to budou délky stran různostranného trojúhelníku? - Rovnoběžník
 Vypočítejte obsah rovnoběžníku ABCD podle obrázku jestliže |70| = 74 cm, |30| = 49 cm a úhel BAD = 60°
Vypočítejte obsah rovnoběžníku ABCD podle obrázku jestliže |70| = 74 cm, |30| = 49 cm a úhel BAD = 60° - Osmiúhelník
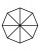 Máme čtverec se stranou 22 cm. Odstřižením rohů máme z něj udělat osmiúhelník. Jaká bude strana osmiúhelníku?
Máme čtverec se stranou 22 cm. Odstřižením rohů máme z něj udělat osmiúhelník. Jaká bude strana osmiúhelníku? - Do kruhu
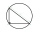 Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku.
Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku. - Podobné trojúhelníky
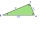 Pravoúhlý trojúhelník ABC má odvěsny a = 5 cm, b = 8 cm. K němu podobný trojúhelník A'B'C' je 2,5krát menší. Vypočítej kolik procent z obsahu trojúhelníku ABC tvoří obsah trojúhelníku A'B'C'.
Pravoúhlý trojúhelník ABC má odvěsny a = 5 cm, b = 8 cm. K němu podobný trojúhelník A'B'C' je 2,5krát menší. Vypočítej kolik procent z obsahu trojúhelníku ABC tvoří obsah trojúhelníku A'B'C'. - Výška stromu podle stínu
 Strom s neznámou výškou vrhá stín dlouhý 18 m, v době, kdy dvoumetrová tyč vrhá stín 2,4m. Jak vysoký je strom?
Strom s neznámou výškou vrhá stín dlouhý 18 m, v době, kdy dvoumetrová tyč vrhá stín 2,4m. Jak vysoký je strom? - Pětiúhelník
 Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20.
Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20. - V trojúhelníku 10
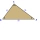 V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC.
V trojúhelníku ABC se velikost vnějšího úhlu při vrcholu C rovná 126°. Velikost vnitřních úhlů při vrcholech A, B jsou v poměru 5: 9. Vypočítej velikost vnitřních úhlů α, β, γ trojúhelníku ABC. - V lichoběžníku
 V lichoběžníku ABCD známe AB = 8 cm, výšku lichoběžníku 6 cm a průsečík úhlopříček je od AB vzdálen 4 cm. Vypočítejte obsah lichoběžníku.
V lichoběžníku ABCD známe AB = 8 cm, výšku lichoběžníku 6 cm a průsečík úhlopříček je od AB vzdálen 4 cm. Vypočítejte obsah lichoběžníku. - Výška letadla
 V jaké výšce letí letadlo, které zaměřil radar pod výškovým úhlem 15°24‘ a přímá vzdálenost letadla od radaru 5545 m?
V jaké výšce letí letadlo, které zaměřil radar pod výškovým úhlem 15°24‘ a přímá vzdálenost letadla od radaru 5545 m? - Reklamní tabule
 Pronájem 1m² reklamní tabule stojí 780 € měsíčně. Reklamní tabule tvaru obdélníku má délku 3m a její úhlopříčka svírá s delší stranou úhel velikosti 34 stupňů. Vypočítejte kolik € podnikatel zaplatí za 4 měsíce pronájmu tabule.
Pronájem 1m² reklamní tabule stojí 780 € měsíčně. Reklamní tabule tvaru obdélníku má délku 3m a její úhlopříčka svírá s delší stranou úhel velikosti 34 stupňů. Vypočítejte kolik € podnikatel zaplatí za 4 měsíce pronájmu tabule. - Podobné trojúhelníky
 Délky stran trojúhelníku ABC jsou v poměru 4:2:5. Vypočítej velikost nejdelší strany jemu podobného trojúhelníku KLM, jehož obvod je 66 cm.
Délky stran trojúhelníku ABC jsou v poměru 4:2:5. Vypočítej velikost nejdelší strany jemu podobného trojúhelníku KLM, jehož obvod je 66 cm. - Vypočítejte výšku
 Vypočítejte obsah a výšku krycí desky tvaru kosodélníku, pro který platí: d(BC)= 60 cm, úhel BAD = 45°, úhel ADB = 90°.
Vypočítejte obsah a výšku krycí desky tvaru kosodélníku, pro který platí: d(BC)= 60 cm, úhel BAD = 45°, úhel ADB = 90°. - Poměr 51
 Poměr vzdálenosti nejbližšího a nejvzdálenějšího bodu kružnice, která je popsána rovnicí x2+y2-16x-12y+75=0 od počátku soustavy souřadnic je?
Poměr vzdálenosti nejbližšího a nejvzdálenějšího bodu kružnice, která je popsána rovnicí x2+y2-16x-12y+75=0 od počátku soustavy souřadnic je? - Obdélníky
 Kolik je obdélníků, jejichž délky stran jsou vyjádřeny přirozenými čísly a mají obsah 8937 cm²?
Kolik je obdélníků, jejichž délky stran jsou vyjádřeny přirozenými čísly a mají obsah 8937 cm²? - Dvě hajovky
 Dvě hajovky A, B jsou odděleny lesem, obě jsou viditelné z myslivny C, která je s oběma spojena přímými cestami. Jakou bude mít délku projektovaná cesta z A do B, je-li AC= 5004 m, BC= 2600 m a úhel ABC= 53°45’?
Dvě hajovky A, B jsou odděleny lesem, obě jsou viditelné z myslivny C, která je s oběma spojena přímými cestami. Jakou bude mít délku projektovaná cesta z A do B, je-li AC= 5004 m, BC= 2600 m a úhel ABC= 53°45’?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
