Planimetrie - slovní úlohy a příklady - strana 160 z 177
Počet nalezených příkladů: 3524
- Raketa
 Vystřelí se raketa rychlostí 100 fps ve směru 30° nad vodorovnou rovinu. Určete maximální výšku, do které stoupá? Fps je jednotka stopa za sekundu.
Vystřelí se raketa rychlostí 100 fps ve směru 30° nad vodorovnou rovinu. Určete maximální výšku, do které stoupá? Fps je jednotka stopa za sekundu. - Na vrcholu
 Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou?
Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou? - Pravděpodobnost na mřížce
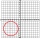 Pravoúhlá mřížka se skládá ze dvou navzájem kolmých soustav rovnoběžných přímek s rozestupem 2. Na tuto rovinu hodíme kruh o průměru 1. Vypočítejte pravděpodobnost, že tento kruh: a) překryje některou z přímek; b) překryje některý z průsečíků přímek?
Pravoúhlá mřížka se skládá ze dvou navzájem kolmých soustav rovnoběžných přímek s rozestupem 2. Na tuto rovinu hodíme kruh o průměru 1. Vypočítejte pravděpodobnost, že tento kruh: a) překryje některou z přímek; b) překryje některý z průsečíků přímek? - Dvě síly
 Dvě síly F1 = 580N a F2 = 630N svírají úhel 59 stupňů. Vypočítejte jejich výslednici F.
Dvě síly F1 = 580N a F2 = 630N svírají úhel 59 stupňů. Vypočítejte jejich výslednici F. - Sínus
 V ▵ ABC, je-li sin (α)= 0,7 a sin (β) = 0,1 vypočítejte sin (γ)
V ▵ ABC, je-li sin (α)= 0,7 a sin (β) = 0,1 vypočítejte sin (γ) - Tramvajová úloha
 Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15. - Úhel mezi úhlopříčkou
 Obdélník má strany 10 cm a 14 cm. Vypočítejte úhel mezi úhlopříčkou a dlouhou stranou.
Obdélník má strany 10 cm a 14 cm. Vypočítejte úhel mezi úhlopříčkou a dlouhou stranou. - V terénu - věta SSU
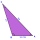 V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele.
V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele. - Pravoúhlý trojúhelník 8
 Pravoúhlý trojúhelník. Je dano: strana b=15,8 úhel alfa =15°11` Výpočtete stranu a, c, úhel beta a obsah
Pravoúhlý trojúhelník. Je dano: strana b=15,8 úhel alfa =15°11` Výpočtete stranu a, c, úhel beta a obsah - Sínus
 Určete nejmenší přirozené číslo p, pro které rovnice 3 sin x = p nemá řešení.
Určete nejmenší přirozené číslo p, pro které rovnice 3 sin x = p nemá řešení. - Nepřístupna místa
 Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji.
Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji. - Vidět harmonický
 Je pravda že velikost střední příčky libovolného lichoběžníku je harmonickým průměrem velikostí jeho základen? Dokažte to. Střední příčka prochází průsečíkem jeho úhlopříček a je rovnoběžná se základnami.
Je pravda že velikost střední příčky libovolného lichoběžníku je harmonickým průměrem velikostí jeho základen? Dokažte to. Střední příčka prochází průsečíkem jeho úhlopříček a je rovnoběžná se základnami. - Strana c
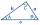 V △ABC a =9, b=6 a ∠ C = 80°. Vypočítejte délku strany c.
V △ABC a =9, b=6 a ∠ C = 80°. Vypočítejte délku strany c. - Vzdálenost cíle
 Cíl C pozorovali ze dvou dělostřeleckých pozorovatelen A, B, které jsou od sebe vzdáleny 975m, přitom velikost úhlu BAC je 63°, velikost ABC je 48°. Vypočítejte vzdálenost bodů A a C.
Cíl C pozorovali ze dvou dělostřeleckých pozorovatelen A, B, které jsou od sebe vzdáleny 975m, přitom velikost úhlu BAC je 63°, velikost ABC je 48°. Vypočítejte vzdálenost bodů A a C. - Západ-jih
 Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž?
Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž? - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - Balón
 Střed balónu je ve výšce 600 m nad zemí. Ze stanoviště na zemí je střed balónu vidět ve výškovém úhlu o velikosti 38° 20´ a balón je pozorován pod zorným úhlem o velikosti 1° 16´. Vypočítejte průměr balónu.
Střed balónu je ve výšce 600 m nad zemí. Ze stanoviště na zemí je střed balónu vidět ve výškovém úhlu o velikosti 38° 20´ a balón je pozorován pod zorným úhlem o velikosti 1° 16´. Vypočítejte průměr balónu. - Spotřeba plechu
 Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,3m. Odchylka strany od roviny podstavy je 36°. Vypočítejte spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad.
Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,3m. Odchylka strany od roviny podstavy je 36°. Vypočítejte spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad. - Úhlopříčka
 Úhlopříčka obdélníku má délku 19,8 cm a svírá s delší stranou úhel 28°. Vypočítejte obsah obdélníku.
Úhlopříčka obdélníku má délku 19,8 cm a svírá s delší stranou úhel 28°. Vypočítejte obsah obdélníku. - V rovině 2
 V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
