Objem + kvadratická rovnice - příklady a úlohy
Počet nalezených příkladů: 52
- Podstavy
 Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav.
Podstavami pravidelného komolého čtyřbokého jehlanu jsou čtverce. Délky stran se liší o 6 dm. Tělesová výška je 7 dm. Objem tělesa je 1813 dm³. Vypočítejte délky hran obou podstav. - Na rovnici paraboly
 V tenisovém zápase je Adrien 5 m od sítě, když odpálí míč vysoký 80 cm od země. Maximální výška jeho parabolické dráhy procházející přes síť byla 1,5 m . Pokud je délka kurtu je 23,77 m, dopadne míček dovnitř kurtu?
V tenisovém zápase je Adrien 5 m od sítě, když odpálí míč vysoký 80 cm od země. Maximální výška jeho parabolické dráhy procházející přes síť byla 1,5 m . Pokud je délka kurtu je 23,77 m, dopadne míček dovnitř kurtu? - Vypočítejte 74834
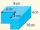 Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199. Vypočítejte hodnotu x.
Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199. Vypočítejte hodnotu x. - Seříznutého 73454
 Objem seříznutého kužele je V=38000π cm³. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy. Určete poloměr podstav, pokud výška v=60 cm.
Objem seříznutého kužele je V=38000π cm³. Poloměr dolní podstavy je o 10 cm větší, než poloměr horní podstavy. Určete poloměr podstav, pokud výška v=60 cm.
- Vypočítejte 70294
 Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem.
Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem. - Rychlostí 65984
 Kámen byl vržen svisle vzhůru rychlostí vo= 15m. s-1. Za jakou dobu bude ve výšce a) 10 m, b) 12 m?
Kámen byl vržen svisle vzhůru rychlostí vo= 15m. s-1. Za jakou dobu bude ve výšce a) 10 m, b) 12 m? - Trojúhelníku 64704
 V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'.
V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'. - Malý Pavel
 Malý Pavel skládal kostky stavebnice (kostka má tvar krychle). Chtěl postavit velikou krychli. Zbylo mu však 75 kostek, proto hranu zvětšil o jednu kostku. Potom mu, ale 16 kostek chybělo. Kolik kostek měl ve stavebnici?
Malý Pavel skládal kostky stavebnice (kostka má tvar krychle). Chtěl postavit velikou krychli. Zbylo mu však 75 kostek, proto hranu zvětšil o jednu kostku. Potom mu, ale 16 kostek chybělo. Kolik kostek měl ve stavebnici? - Vypočítejte 62864
 Objem kvádru je 1440 cm3, jeho povrch je 792 cm² a obsah jedné jeho stěny je 92 cm². Vypočítejte délky jeho stran.
Objem kvádru je 1440 cm3, jeho povrch je 792 cm² a obsah jedné jeho stěny je 92 cm². Vypočítejte délky jeho stran.
- Roviny bočních stěn
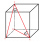 Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’
Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Povrch
 Povrch válce je 1570 cm², jeho výška je 15cm. Určete jeho objem a poloměr podstavy.
Povrch válce je 1570 cm², jeho výška je 15cm. Určete jeho objem a poloměr podstavy. - Komolý
 Komolý pravidelný čtyřboký jehlan má objem 74 cm3, výšku v = 6 cm a obsah dolní podstavy o 15 cm² větší než obsah horní podstavy. Vypočítejte obsah horní podstavy.
Komolý pravidelný čtyřboký jehlan má objem 74 cm3, výšku v = 6 cm a obsah dolní podstavy o 15 cm² větší než obsah horní podstavy. Vypočítejte obsah horní podstavy. - Kvádr
 Kvádr, jehož hrany tvoří tři za sebou jdoucí členy GP, má povrch 112 cm². Součet hran, které procházejí jedním vrcholem je 14 cm. Vypočítejte objem tohoto kvádru.
Kvádr, jehož hrany tvoří tři za sebou jdoucí členy GP, má povrch 112 cm². Součet hran, které procházejí jedním vrcholem je 14 cm. Vypočítejte objem tohoto kvádru. - Povrch pláště , objem
 V rotačním válci je dáno: povrch pláště (bez podstav) S = 96 cm² a objem V = 192 cm krychlových. Vypočítejte poloměr a výšku tohoto válce.
V rotačním válci je dáno: povrch pláště (bez podstav) S = 96 cm² a objem V = 192 cm krychlových. Vypočítejte poloměr a výšku tohoto válce.
- V rotačním válci
 V rotačním válci je dáno: povrch S = 96 cm² a objem V = 192 cm krychlových. Vypočtěte jeho poloměr a výšku.
V rotačním válci je dáno: povrch S = 96 cm² a objem V = 192 cm krychlových. Vypočtěte jeho poloměr a výšku. - Kužel těžký
 Povrch kužele je 200 cm², jeho výška je 7 centimetrů. Spočítej objem tohoto kužele.
Povrch kužele je 200 cm², jeho výška je 7 centimetrů. Spočítej objem tohoto kužele. - Kvádr 55
 Kvádr má objem 1728 cm³ . Určete délky hran a, b, c kvádrů pro které plati a < b < c a a+b+c=38 cm a jejichž číselné hodnoty v cm představují tři po sobě jdoucí členy geometrické posloupnosti.
Kvádr má objem 1728 cm³ . Určete délky hran a, b, c kvádrů pro které plati a < b < c a a+b+c=38 cm a jejichž číselné hodnoty v cm představují tři po sobě jdoucí členy geometrické posloupnosti. - V bazénu
 V bazénu tvaru kvádru je 140 m krychlových vody. Určete rozměry dna, pokud je hloubka vody 200 cm a jeden rozměr dna je o 3 m větší než druhý. Jaké jsou rozměry dna bazénu?
V bazénu tvaru kvádru je 140 m krychlových vody. Určete rozměry dna, pokud je hloubka vody 200 cm a jeden rozměr dna je o 3 m větší než druhý. Jaké jsou rozměry dna bazénu? - Válec obsah pláště
 Válec má obsah pláště 300 cm čtverečních, přičemž výška válce je 12 cm. Vypočítejte objem tohoto válce.
Válec má obsah pláště 300 cm čtverečních, přičemž výška válce je 12 cm. Vypočítejte objem tohoto válce.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
Hledáte pomoc s výpočtem kořenů kvadratické rovnice? Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu. Objem - příklady. příklady na kvadratické rovnice.
