Petr a Franta
Petr a Franta házeli na koš. Každý měl 20 pokusů. Petr se trefil třináctkrát a Franta dvanáctkrát. Vyjádři jejich úspěšnost v procentech.
Správná odpověď:

Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Chceš si dát spočítat kombinační číslo?
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Chceš si dát spočítat kombinační číslo?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Pozorovatel 11
 Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů.
Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů. - Vzdálenost 145
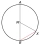 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Kruh - úseč
 Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče. - Na otázku
 Na otázku v anketě odpovědělo kladně 2 312 účastníků, což představuje 68 % celkového počtu účastníků ankety. Určete, kolik měla anketa celkem účastníků.
Na otázku v anketě odpovědělo kladně 2 312 účastníků, což představuje 68 % celkového počtu účastníků ankety. Určete, kolik měla anketa celkem účastníků.
- Prázdne pokoje
 V turistické ubytovně spalo 44 žáků v osmi pokojích, některé byly čtyřlůžkové, jiné šesti lůžkové, Kolik čtyřlůžkových a kolík šesti lůžkových pokojů bylo v ubytovně, když dvě lůžka byla prázdná?
V turistické ubytovně spalo 44 žáků v osmi pokojích, některé byly čtyřlůžkové, jiné šesti lůžkové, Kolik čtyřlůžkových a kolík šesti lůžkových pokojů bylo v ubytovně, když dvě lůžka byla prázdná? - V důsledku
 V důsledku zvýšení produktivity práce o 15% začal podnik vyrábět 920 výrobků za měsíc. Kolik výrobků vyráběl měsíčně předtím?
V důsledku zvýšení produktivity práce o 15% začal podnik vyrábět 920 výrobků za měsíc. Kolik výrobků vyráběl měsíčně předtím? - Číslo 40
 Číslo 112 rozděl na tři složky x, y, z tak, aby platilo x : y = 7 : 5 a y : z = 3 : 4.
Číslo 112 rozděl na tři složky x, y, z tak, aby platilo x : y = 7 : 5 a y : z = 3 : 4. - Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Produkce
 Měsíční produkce podniku se zvýšila z 352 výrobků na 528 výrobků. O kolik procent tedy původní měsíční produkce vzrostla?
Měsíční produkce podniku se zvýšila z 352 výrobků na 528 výrobků. O kolik procent tedy původní měsíční produkce vzrostla?
- Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Peleton
 Při cyklistických závodech jede peleton průměrnou rychlostí 36 km/h. Opravovou defektu se jeden závodník zdržel 5 minut. O kolik kilometrů za hodinu byla pak jeho rychlost větší než rychlost peletonu když ho dostihl za 20 minut? Jak dlouho by mu trvalo kd
Při cyklistických závodech jede peleton průměrnou rychlostí 36 km/h. Opravovou defektu se jeden závodník zdržel 5 minut. O kolik kilometrů za hodinu byla pak jeho rychlost větší než rychlost peletonu když ho dostihl za 20 minut? Jak dlouho by mu trvalo kd - Ovoce 7
 Cena 6 kg hrušek je o 77 Kč vyšší než cena 5 kg jablek. Cena 6 kg jablek je stejná jako cena 5 kg hrušek. Kolik stojí 2 kg jablek?
Cena 6 kg hrušek je o 77 Kč vyšší než cena 5 kg jablek. Cena 6 kg jablek je stejná jako cena 5 kg hrušek. Kolik stojí 2 kg jablek? - Evelína 2
 Evelína zryje zahradu za 4 hodiny. Její kamarádka Doubravka to zvládne za tři hodiny. Evelína začala pracovat ve 13 hodin a hodinu později se k ní přidala Doubravka, aby se spolu mohly jít koupat. Vypočítejte, v kolik hodin budou moci dívky odejít na koup
Evelína zryje zahradu za 4 hodiny. Její kamarádka Doubravka to zvládne za tři hodiny. Evelína začala pracovat ve 13 hodin a hodinu později se k ní přidala Doubravka, aby se spolu mohly jít koupat. Vypočítejte, v kolik hodin budou moci dívky odejít na koup - Známky 5
 Známky se stejnou vahou 2,1,3,2,2,3,1,3,1,1,2,4,2,2,3,1,1,2,1,3 urči: 1) aritmetický průměr 2) absolutní a relativní četnost 3) modus a medián 4) vytvoř graf
Známky se stejnou vahou 2,1,3,2,2,3,1,3,1,1,2,4,2,2,3,1,1,2,1,3 urči: 1) aritmetický průměr 2) absolutní a relativní četnost 3) modus a medián 4) vytvoř graf
- Vykrátiť 2
 Vyhodnotťe nasledovný výraz s faktoriálmi: (45!-44!)/(44!)
Vyhodnotťe nasledovný výraz s faktoriálmi: (45!-44!)/(44!) - Krize
 Firma během krize propouštěla zaměstnance, takže jich měla na konci krize o 40 % méně než před krizí. Když firma po odeznění krize přijala 42 nových zaměstnanců, měla jich o 25 % více než na konci krize. Kolik zaměstnanců měla firma před krizí?
Firma během krize propouštěla zaměstnance, takže jich měla na konci krize o 40 % méně než před krizí. Když firma po odeznění krize přijala 42 nových zaměstnanců, měla jich o 25 % více než na konci krize. Kolik zaměstnanců měla firma před krizí? - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
