Normální rozložení
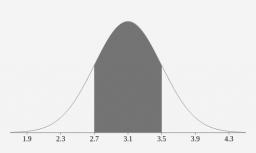
Na jedné střední škole jsou známky normálně distribuovány s průměrem 3,1 a směrodatnou odchylkou 0,4. Jaké procento studentů na vysoké škole mají známky mezi 2,7 a 3,5?
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem aritmetického průměru?
Hledáte statistickou kalkulačku?
Hledáte kalkulačku směrodatné odchylky?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Chceš si dát spočítat kombinační číslo?
Hledáte statistickou kalkulačku?
Hledáte kalkulačku směrodatné odchylky?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Chceš si dát spočítat kombinační číslo?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Předpokládejme 78684
 Předpokládejme, že výška chlapce je normálně rozdělena se střední hodnotou 60 palců a směrodatnou odchylkou 10. Jaké procento chlapcovy výšky bychom očekávali mezi 44 a 75 a méně než 49 a 76 a více?
Předpokládejme, že výška chlapce je normálně rozdělena se střední hodnotou 60 palců a směrodatnou odchylkou 10. Jaké procento chlapcovy výšky bychom očekávali mezi 44 a 75 a méně než 49 a 76 a více? - Distribuována 6419
 Průměrná GPA (Grade Point Average = průměr známek) je 2,78 se standardní odchylkou 0,45. Pokud je GPA normálně distribuována, jaké procento studentů má následující GPA? Vyřešte pomocí Z-skóre a nahlaste příslušné procento: a. Méně než 2,30 b. Méně než 2,0
Průměrná GPA (Grade Point Average = průměr známek) je 2,78 se standardní odchylkou 0,45. Pokud je GPA normálně distribuována, jaké procento studentů má následující GPA? Vyřešte pomocí Z-skóre a nahlaste příslušné procento: a. Méně než 2,30 b. Méně než 2,0 - Standardní 83165
 Skóre IQ je normálně rozděleno s průměrem 100 a standardní odchylkou 15. Jaké procento populace má v IQ testu skóre vyšší než 125?
Skóre IQ je normálně rozděleno s průměrem 100 a standardní odchylkou 15. Jaké procento populace má v IQ testu skóre vyšší než 125? - Předpokládejme 80688
 Předpokládejme, že skóre v testu má normální rozdělení se střední hodnotou X=74 a standardní odchylkou s=18. Jaké procento studentů má skóre vyšší než 90? Jaké procento studentů má skóre mezi 70 a 85? Dvacet procent studentů dělá lepší, než dosáhli na zko
Předpokládejme, že skóre v testu má normální rozdělení se střední hodnotou X=74 a standardní odchylkou s=18. Jaké procento studentů má skóre vyšší než 90? Jaké procento studentů má skóre mezi 70 a 85? Dvacet procent studentů dělá lepší, než dosáhli na zko
- Významnosti 49413
 Výrobce baterií do telefonů tvrdí, že životnost jeho baterií je přibližně normálně rozdělena se standardní odchylkou 0,9 roku. Pokud náhodný vzorek 10 těchto baterií má směrodatnou odchylku 1,2 roku. Myslíte si, že směrodatná odchylka je větší než 0,9 rok
Výrobce baterií do telefonů tvrdí, že životnost jeho baterií je přibližně normálně rozdělena se standardní odchylkou 0,9 roku. Pokud náhodný vzorek 10 těchto baterií má směrodatnou odchylku 1,2 roku. Myslíte si, že směrodatná odchylka je větší než 0,9 rok - Spravedlivých 80479
 Při přijímací zkoušce na vysokou školu jsou účastníci hodnoceni jako výborní, velmi dobří, dobří a spravedliví. Zvažte, že skóre ve zkoušce je normálně rozděleno s průměrem 78 a standardní odchylkou 7,5. Účastníci, kteří získají prvních 5 % bodů, budou ho
Při přijímací zkoušce na vysokou školu jsou účastníci hodnoceni jako výborní, velmi dobří, dobří a spravedliví. Zvažte, že skóre ve zkoušce je normálně rozděleno s průměrem 78 a standardní odchylkou 7,5. Účastníci, kteří získají prvních 5 % bodů, budou ho - Směrodatnou 32751
 Tabulka je uvedena: dní stížnosti 0-4 2 5-9 4 10-14 8 15-19 6 20-24 4 25-29 3 30-34 3 1,1 Jaké procento stížností bylo vyřešeno do 2 týdnů? 1,2 vypočítat průměrný počet dní na vyřešení těchto stížností. 1,3 vypočítat modální počet dní pro vyřešení těchto
Tabulka je uvedena: dní stížnosti 0-4 2 5-9 4 10-14 8 15-19 6 20-24 4 25-29 3 30-34 3 1,1 Jaké procento stížností bylo vyřešeno do 2 týdnů? 1,2 vypočítat průměrný počet dní na vyřešení těchto stížností. 1,3 vypočítat modální počet dní pro vyřešení těchto - Pravděpodobnost 73204
 Předpokládejme, že životnost revoluční žárovky je normálně rozložena se střední životností 70 tisíc hodin a směrodatnou odchylkou 3 tisíc hodin. Pokud se žárovka vyjme náhodně: a) jaká je pravděpodobnost, že délka života bude do 5 000 hodin od průměru; b)
Předpokládejme, že životnost revoluční žárovky je normálně rozložena se střední životností 70 tisíc hodin a směrodatnou odchylkou 3 tisíc hodin. Pokud se žárovka vyjme náhodně: a) jaká je pravděpodobnost, že délka života bude do 5 000 hodin od průměru; b) - Specialista 72844
 Roční plat odborníka na statistiku na základní úrovni (v tisících dolarů) je normálně rozdělen s průměrem 75 a standardní odchylkou 12. X ∼ N ( μ = 75, σ = 12 ). Jaká je minimální mzda, na kterou by se měl specialista statistiky zaměřit, aby vydělal mezi
Roční plat odborníka na statistiku na základní úrovni (v tisících dolarů) je normálně rozdělen s průměrem 75 a standardní odchylkou 12. X ∼ N ( μ = 75, σ = 12 ). Jaká je minimální mzda, na kterou by se měl specialista statistiky zaměřit, aby vydělal mezi
- Předpokládejme 16
 Předpokládejme, že se IQ v populaci řídí normálním rozdělením se střední hodnotou 100 bodů a směrodatnou odchylkou 10 bodů. S jakou pravděpodobností mezi 15 náhodně vybranými lidmi: a. Není nikdo s IQ nad 130 bodů? b. Jsou alespoň 2 lidé s IQ nad 130 bodů
Předpokládejme, že se IQ v populaci řídí normálním rozdělením se střední hodnotou 100 bodů a směrodatnou odchylkou 10 bodů. S jakou pravděpodobností mezi 15 náhodně vybranými lidmi: a. Není nikdo s IQ nad 130 bodů? b. Jsou alespoň 2 lidé s IQ nad 130 bodů - Pravděpodnost 27981
 Při hromadné výrobě výrobku je průměrný rozměr 250mm, přičemž rozměry jednotlivých výrobků vlivem nepřesností při výrobě kolísají kolem této střední hodnoty. Rozměr výrobků má normální rozdělení se směrodatnou odchylkou a=10mm a) Jaká je pravděpodnost, že
Při hromadné výrobě výrobku je průměrný rozměr 250mm, přičemž rozměry jednotlivých výrobků vlivem nepřesností při výrobě kolísají kolem této střední hodnoty. Rozměr výrobků má normální rozdělení se směrodatnou odchylkou a=10mm a) Jaká je pravděpodnost, že - Vypracování 67074
 Čas potřebný k vypracování testu má normální rozdělení se střední hodnotou 50 minut a směrodatnou odchylkou 10 minut. Kolik procent studentů vypracuje test do 30 minut?
Čas potřebný k vypracování testu má normální rozdělení se střední hodnotou 50 minut a směrodatnou odchylkou 10 minut. Kolik procent studentů vypracuje test do 30 minut? - Pravděpodobnost 74714
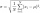 Váhy ryb v určitém jezeře je normálně rozdělena o průměru 11 lb (liber) a standardní odchylkou 6 lb. Pokud jsou náhodně vybrány 4 ryby, jaká je pravděpodobnost, že průměrná hmotnost bude mezi 8,6 a 14,6 lb? Vaši odpověď zaokrouhlete na čtvrté desetinné mí
Váhy ryb v určitém jezeře je normálně rozdělena o průměru 11 lb (liber) a standardní odchylkou 6 lb. Pokud jsou náhodně vybrány 4 ryby, jaká je pravděpodobnost, že průměrná hmotnost bude mezi 8,6 a 14,6 lb? Vaši odpověď zaokrouhlete na čtvrté desetinné mí - IQ - normálne rozdelenie
 Inteligenční kvocient, (IQ), je standardizované skóre používané jako výstup standardizovaných inteligenčních psychologických testů k vyčíslení inteligence člověka v poměru k ostatní populaci (respektive k dané skupině). Inteligence má přibližně normální r
Inteligenční kvocient, (IQ), je standardizované skóre používané jako výstup standardizovaných inteligenčních psychologických testů k vyčíslení inteligence člověka v poměru k ostatní populaci (respektive k dané skupině). Inteligence má přibližně normální r
- Na univerzitě
 Na určité univerzitě je 25% studentů obchodní fakulty. Ze studentů obchodní fakulty je 66% mužů. Avšak pouze 52% všech studentů na univerzitě jsou muži. a. Jaká je pravděpodobnost, že náhodně vybraný student na univerzitě je muž na obchodní fakultě? b. Ja
Na určité univerzitě je 25% studentů obchodní fakulty. Ze studentů obchodní fakulty je 66% mužů. Avšak pouze 52% všech studentů na univerzitě jsou muži. a. Jaká je pravděpodobnost, že náhodně vybraný student na univerzitě je muž na obchodní fakultě? b. Ja - Pravděpodobnost 80623
 Při testování skupině studentů jsou níže shrnuty známky a pohlaví. Známky a pohlaví ; A; B ; C ; Celkem Muž; 20; 6; 19 ; 45 Žena ; 17; 18; 13; 48 Celkem; 37; 24; 32; 93 Je-li náhodně vybrán jeden student, a) Najděte pravděpodobnost, že student dostal B. b
Při testování skupině studentů jsou níže shrnuty známky a pohlaví. Známky a pohlaví ; A; B ; C ; Celkem Muž; 20; 6; 19 ; 45 Žena ; 17; 18; 13; 48 Celkem; 37; 24; 32; 93 Je-li náhodně vybrán jeden student, a) Najděte pravděpodobnost, že student dostal B. b - Významnosti 49483
 Profesor na hodině strojopisu zjistil, že průměrný výkon zkušeného písaře je 85 slov za minutu. Náhodný vzorek 16 studentů absolvoval test na psaní a dosáhlo průměrné rychlosti 62 slov za minutu se standardní odchylkou 8. Můžeme říci, že výkony studentů v
Profesor na hodině strojopisu zjistil, že průměrný výkon zkušeného písaře je 85 slov za minutu. Náhodný vzorek 16 studentů absolvoval test na psaní a dosáhlo průměrné rychlosti 62 slov za minutu se standardní odchylkou 8. Můžeme říci, že výkony studentů v
