Uhol priamky a roviny

Určte uhol priamky, ktorá je určená parametricky x=5+t y=1+3t z=-2t t patri R a roviny, ktorá je určená všeobecnou rovnicou 2x-y+3z-4=0.

Správna odpoveď:

X =  30 °

Postup správneho riešenia:

S=(1,3,−2) N=(2,−1,3)  p = S , N p=Sx​⋅ Nx​+Sy​⋅ Ny​+Sz​⋅ Nz​=1⋅ 2+3⋅ (−1)+(−2)⋅ 3=−7  s=∣S∣=Sx2​+Sy2​+Sz2​​=12+32+(−2)2​=14​≐3,7417  n=∣N∣=Sx2​+Sy2​+Sz2​+Nx2​+Ny2​+Nz2​​=12+32+(−2)2+22+(−1)2+32​=14​≐3,7417  cos A =  ∣S∣,∣N∣∣p∣​  A=π180°​⋅arccos(s⋅ n∣p∣​)=π180°​⋅arccos(3,7417⋅ 3,7417∣(−7)∣​)=60 ∘ X=90−A=90−60=30∘=30°

Skúsiť iný príklad


Našiel si chybu či nepresnosť? Prosím nám ju pošli.



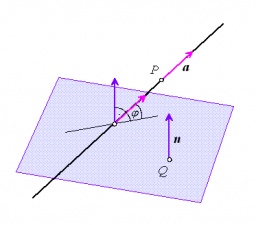
Zobrazujem 1 komentár:
Dr Math
Uhol priamky a roviny, analytická geometria

https://www.youtube.com/watch?v=DRPHkr8e2fI





Tipy na súvisiace online kalkulačky
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:

geometriaaritmetikaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy

 
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1   video2   video3

Súvisiace a podobné príklady: