Parametrický tvar
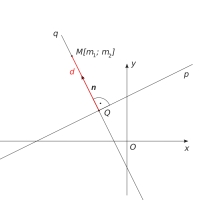
Vypočítajte vzdialenosť bodu A [2,1] od priamky p:
X = -1 + 3t
Y = 5-4t
Priamka p má parametrický tvar rovnica priamky. ..
X = -1 + 3t
Y = 5-4t
Priamka p má parametrický tvar rovnica priamky. ..
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- analytická geometria
- vektor
- skalárny súčin
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- trojuholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Osová súmernosť
Vypočítajte súradnice bodu B osovo symetricky s bodom A [-1, -3] pozdĺž priamky p: x + y - 2 = 0. - Všeobecná rovnica
Vo všetkých príkladoch napíšte VŠEOBECNÚ rovnicami priamky, ktorá je nejakým spôsobom zadaná. A) priamka je daná parametricky: x = - 4 + 2p; y = 2 - 3p B) priamka je daná smernicovým tvarom: y = 3x - 1 C) priamka je daná dvomi bodmi: A [3; -3], B [-5; 2] - Vzdialenosť
Vypočítajte vzdialenosť bodu A [0, 2] od priamky prechádzajúcej bodmi B [9, 5] a C [1, -1]. - Na priamke
Na priamke p: x = 4 + t, y = 3 + 2t, t sú R, určte bod C, ktorý má rovnakú vzdialenosť od bodov A [1,2] a B [-1,0]. - Kolmý priemet Určte vzdialenosť bodu B [1, -3] od kolmého priemetu bodu A [3, -2] na priamku 2 x + y + 1 = 0.
- Smernicový tvar
Nájdite rovnicu priamky prechádzajúcu bodom X [2, 5] a sklonom - smernicou -0,3. Odpoveď zapíšte v tvare y = ax + b, kde a, b sú konštanty. - Osová súmernosť
Nájdite obraz A 'bodu A [1,2] v osovej súmernosti s osou p: x = -1 + 3t, y = -2 + t (t = sú reálne čísla) - Vzdialenosť rovnobežiek
Zistite vzdialenosť rovnobežiek, ktorej rovnice sú: x=3-4t, y=2+t a x=-4t, y=1+t (návod:na jednej priamke zvoľte bod a zistite jeho vzdialenosť od druhej priamky) - Dotyčnice a elipsa
Nájdite veľkosť uhla, pod ktorým je elipsa x² + 5 y² = 5 viditeľná z bodu P [5, 1]. - Na priamke
Na priamke p: 3 x - 4 y - 3 = 0, stanovte súradnice bodu C, ktorý je rovnako vzdialený od bodov A [4, 4] a B [7, 1]. - Súradnice vrcholov
Určte súradnice vrcholov a obsah rovnobeznika, ktoreho dve strany ležia na priamkach 8x+3y+1=0, 2x+y-1=0 a uhlopriečka na priamke 3x+ 2y+3=0 - Uhol priamky a roviny
Určte uhol priamky, ktorá je určená parametricky x=5+t y=1+3t z=-2t t patri R a roviny, ktorá je určená všeobecnou rovnicou 2x-y+3z-4=0. - Priamka a úsečka
Rozhodnite, či priamka p: x + 2 y - 7 = 0 pretína úsečku danú bodmi A [1, 1] a B [5, 3] - Bod A Bod A [6 ; -2] . Bod B = [-3 ; 1] Zapíš parametrické vyjadrenie úsečky BA tak, aby t patrilo do uzavretý interval < 0;3 >
- Vypočítajte 32
Vypočítajte príklad s desatinnými číslami: -5+(-14+11)•[24-2•(-0,4)]-{-28-41•[-8•2+4•1•(0,1-2,4)]+1}= - Parametrické 33451 Priamka p je daná bodom P [ - 0,5;1] a smerovým vektorom s= (1,5; - 3) určite: A) hodnotu parametra t pre body X [- 1,5;3], Y [1; - 2] priamky p B) či body R [0,5; - 1], S [1,5;3] leží na priamke p C) parametrické rovnice priamky m || p, ak prechádza pria
- Priamka
Daná je priamka, ktorá prechádza bodmi A [–3; 22] a B [33; –2]. Určte počet všetkých bodov tejto priamky, ktorých obidve súradnice sú kladné celé čísla.
