Nekonečno
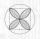
Do štvorca o strane dĺžky 18 je vpísaný kruh, do neho potom štvorec, do toho opäť kruh atď. do nekonečna. Vypočítajte súčet obsahov všetkých týchto štvorcov.
Správna odpoveď:
Zobrazujem 2 komentáre:
Žiak
Myslím, že tento príklad, je zle vyriešený, q má byť v tomto príklade 1/4. Keď by som si vypočítala S2, tak je to (25/2) 2 teda 625/4 a keď dám do pomeru S2 a S1, tak q = 1/4. Potom súčet všetkých obsahov je 2500/3
Jakub
nemate asi pravdu, q=1/2... rozpisal som riesenie... uhlopriecka stvorca je odmocnina z 2 krat strana ... q = (1/sqrt(2))2 = 1/2
Kruh ma priemer rovny dlzke strany stvorca a vpisany stvorec ma uhlopriecku = priemeru.
Kruh ma priemer rovny dlzke strany stvorca a vpisany stvorec ma uhlopriecku = priemeru.
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikaplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Do štvorca
Do štvorca so stranou 12 cm je vpísaný kruh tak, že sa dotýka všetkých jeho strán. Vypočítajte rozdiel obsahov štvorca a kruhu. - Rekurzia štvorca
Do štvorca ABCD je vpísaný štvorec tak, že jeho vrcholy ležia v stredoch strán štvorca ABCD; tomu je vpísaný štvorec rovnakým spôsobom. Postup sa opakuje. Dĺžka strany štvorca ABCD je a = 12 cm. Aký veľký je: a) súčet obvodov všetkých štvorcov, b) súčet o - Obvod kruhu
Vypočítajte obvod kruhu v dm, ktorého polomer sa rovná strane štvorca s obsahom 0,49 dm²? - Kruhy
Obsah kruhu vpísaného do štvorca je 18. Aký je obsah kruhu opísaného okolo štvorca? - Štvorlístok
Vypočítajte obsah štvorlístka, ktorý je vpísaný do štvorca, ktorého strana má dĺžku 6 cm. - Opísaný 4187
Určite obsah kruhu, ktorý je a) vpísaný, b) opísaný štvorci o strane 6,32 cm. - Trojuholníky
Daný je štvorec ABCD a na každej jeho strane je zvolených n jej vnútorných bodov. Určte počet všetkých trojuholníkov, ktorých vrcholy X, Y, Z ležia v týchto bodoch a na rôznych stranách štvorca.
