Stĺp
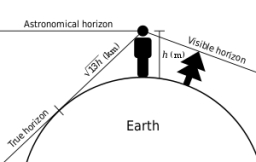
Stĺpik má 13 metrov dlhý tieň na svahu stúpajúcom od stožiara stĺpika v smere uhla tieňa pri uhle 15°. Určte výšku stĺpiku, ak je slnko nad obzorom (horizontom) v uhle 33°. Použite sínusovú vetu .
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Chcete premeniť jednotku dĺžky?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- geometria
- podobnosť trojuholníkov
- planimetria
- pravouhlý trojuholník
- trojuholník
- sínusová veta
- goniometria a trigonometria
- sínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Stožiar
Stožiar elektrického vedenia vrhá 15 m dlhý tieň na stráň ktorá stúpa od päty stožiaru v smere tieňa pod uhlom o veľkosti 11,5° Určte výšku stožiaru, ak výška Slnka nad obzorom je daná uhlom 38°36'. - Slnečné hodiny
Tyč je zvisle zabodnutá do zeme. Vyčnievajúca dĺžka je 1m. Aká je dĺžka vrhnutého tieňa, keď je slnko práve 50° nad horizontom? - Dva trojuholníky SSU
Dva trojuholníky môžu byť vytvorené z uvedených informácií. Použite sínusovú vetu na riešenie trojuholníkov: A = 59°, a = 13, b = 14 - Vypočítajte 253
Vypočítajte výšku stožiaru, ktorého pätu vidíme v hĺbkovom uhle 11° a vrchol vo výškovom uhle 28°. Stožiar je pozorovaný z miesta 10 m nad úrovňou päty stožiara.
- Lietadlo 13
Lietadlo letiace práve nad miestom A vidieť z pozorovateľne B, vzdialenej od miesta A 2 400 metrov, vo výškovom uhle 52°30´. Ako vysoko letí lietadlo? - Vzdialenosť 83872
Muž stojaci na palube lode, ktorá je 10 m nad hladinou vody, pozoruje vrchol kopca pri uhle elevácie 60 ° a pozorovací uhol sklonu päty kopca je 30 °. Nájdite vzdialenosť kopca od lode a výšku kopca. - Výškový uhol
Približne v akej výške je mrak, ktorý vidíme pod výškovým uhlom 26° 10' ak vidíme slnko pod výškovým uhlom 29° 15' a tieň mraku je od nás vzdialený 92 metrov?
