Rovnoramenný trojuholník -VU
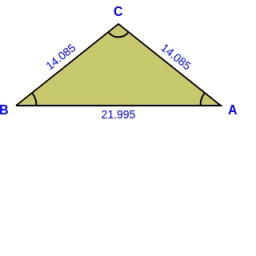
Vypočítajte dĺžky strán v rovnoramennom trojuholníku, ak je dana výška (na základňu) Vc= 8,8cm a uhol pri zakladni alfa= 38°40`.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Chcete premeniť jednotku dĺžky?
Vypočet rovnoramenného trojuholníka.
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Chcete premeniť jednotku dĺžky?
Vypočet rovnoramenného trojuholníka.
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- planimetria
- pravouhlý trojuholník
- trojuholník
- základné funkcie
- percentá
- goniometria a trigonometria
- sínus
- kosínus
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Vypočítajte 7
Vypočítajte dĺžku zvyšných dvoch strán a veľkosť uhlov v pravouhlom trojuholníku ABC, ak a=10 cm, uhol alfa = 18°40' . - Trojuholníku 6568
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C je dané : a=17cm, Vc=8 cm. Vypočítajte dĺžku strán b, c, jeho obsah S, obvod o, dĺžku polomerov kružníc trojuholníka opísané R a vpísané r a veľkosť uhlov alfa a beta. - Rovnoramennom 82143
Urči veľkosť vnútorných uhlov v rovnoramennom trojuholníku, ak vieš, že uhol ležiaci proti základni je o 15° väčší ako uhly pri základni. - Rovnoramenný lichobežník
V rovnoramennom lichobežníka ABCD, AB||CD, je |CD| = c = 11 cm, výška v = 16 cm, | CAB | = 38°. Vypočítaj obsah lichobežníka.
- V rovnoramennom 3
V rovnoramennom trojuholníku je uhol pri vrchole o 30° väčší ako uhol pri základni. Aké veľké sú vnútorné uhly? - Strany z výšky
Vypočítaj veľkosť strán a uhlov trojuholníka ABC, ak poznáš vc = 28, α = 51°19', β = 67°38'. - Rovnoramennom 23271
V rovnoramennom trojuholníku je veľkosť uhla pri hlavnom vrchole o 20° menšia ako dvojnásobná veľkosť uhla pri základni. Aké sú vnútorné uhly trojuholníka? - V rovnoramennom 7
V rovnoramennom trojuholníku je strana a=b= 21 cm, výška trojuholníka je 19 cm. Zisti základňu a obvod trojuholníka (náčrt, výpočet, odpoveď). - Pravouhlý
Pravouhlý trojuholník KLM s pravým uhlom pri vrchole L, uhľom beta pri vrchole K a uhľom alfa u vrchole M. Uhol pri vrchole M = 65°, strana l = 17,5 cm. Pomôcť Pytagorovy vety a goniometrických funkciu vypočítate dĺžky všetkých strán a uhol pri vrchole K.
- RR lichobežník
V rovnoramennom lichobežníku ABCD má rameno dĺžku 5,2 cm, stredná priečka má dĺžku 7 cm a výška sa rovná 4,8 cm. Vypočítajte dĺžky oboch základní. - Ťažisko
V rovnoramennom trojuholníku ABC je pomer dĺžok základne AB a výšky na základňu 10:12. Rameno má dĺžku 26 cm. Ak je T ťažiskom trojuholníka ABC, vypočítajte obsah trojuholníka ABT. - RR trojuholník XYZ
Rovnoramenný trojuholník XYZ má základňu z = 10 cm. Uhol oproti základni je súčtom uhlov pri základni. Vypočítajte obsah trojuholníka XYZ. - Trojuholníku 9701
V trojuholníku je daná dĺžka strany AB = 6 cm, výška na stranu c = 5 cm, uhol BCA = 35°. Vypočítajte strany a, b. - Vypočítajte 53
Vypočítajte obsah trojuholníka ABC, ak je dané alfa=49°, beta=31° a výška na stranu c je 9cm.
- Rameno
V rovnoramennom trojuholniku s obvodom 36 cm má výška na základňu dĺžku 12 cm. Vypočítaj dĺžku ramena daného trojuholníka. - Narysujte
Narysujte rovnoramenný trojuholník ABC, ak AB=7cm, veľkosť uhla ABC je 47°, ramená |AC| = |BC|. Odmerajte veľkosť strany BC v mm. - V trojuholníku 5
V trojuholníku ABC platí, že výška na stranu a je 6cm. Výška na stranu b sa rovná 9 cm. Strana "a" je o 4cm dlhšia ako strana "b". Vypočítajte dĺžky strán a, b.
