Neznáme číslo
Neznáme číslo je deliteľné práve tromi rôznymi prvočíslami. Keď tieto prvočísla porovnáme vzostupne, platí nasledujúce:
• Rozdiel druhého a prvého prvočísla je polovicou rozdielu tretieho a druhého prvočísla.
• Súčin rozdielu druhého a prvého prvočísla s rozdielom tretieho a druhého prvočísla je násobkom 17.
Určte najmenšie číslo, ktoré má všetky vyššie uvedené vlastnosti.
• Rozdiel druhého a prvého prvočísla je polovicou rozdielu tretieho a druhého prvočísla.
• Súčin rozdielu druhého a prvého prvočísla s rozdielom tretieho a druhého prvočísla je násobkom 17.
Určte najmenšie číslo, ktoré má všetky vyššie uvedené vlastnosti.
Správna odpoveď:

Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Štyri čísla
 Nájdite také štyri čísla, ktorých súčet je 48 a ktoré majú tieto vlastnosti: ked od prvého odčítame 3, k druhému pripočítame 3, tretie vynásobíme tromi a štvrté vydelíme tromi, dostaneme rovnaký výsledok.
Nájdite také štyri čísla, ktorých súčet je 48 a ktoré majú tieto vlastnosti: ked od prvého odčítame 3, k druhému pripočítame 3, tretie vynásobíme tromi a štvrté vydelíme tromi, dostaneme rovnaký výsledok. - Neznáme 30
 Neznáme číslo zmenším o 5 a výsledný rozdiel vynásobím tromi. Nakoniec výsledný súčin zväčším o 6 a dostanem najmenší spoločný násobok čísel 3 a 8. Vypočítaj neznáme číslo.
Neznáme číslo zmenším o 5 a výsledný rozdiel vynásobím tromi. Nakoniec výsledný súčin zväčším o 6 a dostanem najmenší spoločný násobok čísel 3 a 8. Vypočítaj neznáme číslo. - MO Z8-I-2 2012
 Číslo X je najmenšie také prirodzené číslo, ktorého polovica je deliteľná tromi, tretina deliteľná štyrmi, štvrtina deliteľná jedenástimi a jeho polovica dáva zvyšok 5 po delení siedmimi. Nájdite toto číslo.
Číslo X je najmenšie také prirodzené číslo, ktorého polovica je deliteľná tromi, tretina deliteľná štyrmi, štvrtina deliteľná jedenástimi a jeho polovica dáva zvyšok 5 po delení siedmimi. Nájdite toto číslo. - Prvočísla 2
 Ktorými prvočíslami je deliteľné číslo 2031?
Ktorými prvočíslami je deliteľné číslo 2031?
- Dve čísla
 Mám dve čísla. Ich súčet je 140. Jedna pätina prvého čísla sa rovná polovici druhého čísla. Určte tieto neznáme čísla.
Mám dve čísla. Ich súčet je 140. Jedna pätina prvého čísla sa rovná polovici druhého čísla. Určte tieto neznáme čísla. - Vynechaná číslica
 Doplňte vynechanú číslicu v čísle 3 ∗ 43 tak, aby vzniklo číslo, ktoré je deliteľné tromi. Ak je viac možností, uveďte všetky. (Vynechaná číslica je označená symbolom ∗. ) Odpovede je treba zdôvodniť!
Doplňte vynechanú číslicu v čísle 3 ∗ 43 tak, aby vzniklo číslo, ktoré je deliteľné tromi. Ak je viac možností, uveďte všetky. (Vynechaná číslica je označená symbolom ∗. ) Odpovede je treba zdôvodniť! - Z7-I-4 MO 2017
 Na stole ležalo šesť kartičiek s ciframi 1, 2, 3, 4, 5, 6. Anežka z týchto kartičiek zložila šesťciferné číslo, ktoré bolo deliteľné šiestimi. Potom postupne odoberala kartičky sprava. Keď odobrala prvú kartičku, zostalo na stole päťciferné číslo deliteľn
Na stole ležalo šesť kartičiek s ciframi 1, 2, 3, 4, 5, 6. Anežka z týchto kartičiek zložila šesťciferné číslo, ktoré bolo deliteľné šiestimi. Potom postupne odoberala kartičky sprava. Keď odobrala prvú kartičku, zostalo na stole päťciferné číslo deliteľn - Dispozícii 8091
 Záhradník má vysadiť tri záhony, každý práve jedným druhom rastlín. Možností, ako vysadiť tieto 3 záhony tromi rôznymi druhmi rastlín, je o 133 menej ako možnosťou, ako je možné tieto záhony vysadiť najviac tromi rôznymi druhmi rastlín. Počet rastlín každ
Záhradník má vysadiť tri záhony, každý práve jedným druhom rastlín. Možností, ako vysadiť tieto 3 záhony tromi rôznymi druhmi rastlín, je o 133 menej ako možnosťou, ako je možné tieto záhony vysadiť najviac tromi rôznymi druhmi rastlín. Počet rastlín každ - Rozdeľte 2
 Rozdeľte štvorec so stranou dĺžky 12 cm na tri obdĺžniky s rovnakými obvodmi tak, aby tieto obvody boli čo najmenšie.
Rozdeľte štvorec so stranou dĺžky 12 cm na tri obdĺžniky s rovnakými obvodmi tak, aby tieto obvody boli čo najmenšie.
- Najmenšie
 Vytvorte najmenšie možné číslo, ktoré je deliteľné číslami 5,8,9,4,3
Vytvorte najmenšie možné číslo, ktoré je deliteľné číslami 5,8,9,4,3 - Rozdiel dvoch čísel
 Rozdiel 2 čísel je 82. Prvé číslo je o 8 menšie ako druhá mocnina druhého čísla. Určte tieto čísla.
Rozdiel 2 čísel je 82. Prvé číslo je o 8 menšie ako druhá mocnina druhého čísla. Určte tieto čísla. - MO C–I–1 2018
 Neznáme číslo je deliteľné práve štyrmi číslami z množiny {6, 15, 20, 21, 70}. Určite, ktorými.
Neznáme číslo je deliteľné práve štyrmi číslami z množiny {6, 15, 20, 21, 70}. Určite, ktorými. - Trojuholníka 4050
 Vypočítajte veľkosť vnútorných uhlov trojuholníka, ak je veľkosť druhého uhla o 120 stupňov menšia ako dvojnásobok veľkosti prvého uhla a veľkosť tretieho uhla sa rovná rozdielu veľkostí prvého a druhého uhla.
Vypočítajte veľkosť vnútorných uhlov trojuholníka, ak je veľkosť druhého uhla o 120 stupňov menšia ako dvojnásobok veľkosti prvého uhla a veľkosť tretieho uhla sa rovná rozdielu veľkostí prvého a druhého uhla. - Tretiu s druhou
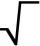 Máme 2 čísla. Keby sme vynásobili tretiu odmocninu prvého čísla s druhou odmocninou druhého čísla, dostali by sme číslo 18.Určte tieto 2 čísla. Ak má úloha v množine reálnych čísel nekonečne veľa riešení, vypočítajte len celočíselné riešenie.
Máme 2 čísla. Keby sme vynásobili tretiu odmocninu prvého čísla s druhou odmocninou druhého čísla, dostali by sme číslo 18.Určte tieto 2 čísla. Ak má úloha v množine reálnych čísel nekonečne veľa riešení, vypočítajte len celočíselné riešenie.
- Aritmetickej 78594
 Súčin tretieho a druhého člena aritmetickej postupnosti je 3000. Ak je spoločný rozdiel 10, nájdite prvý člen.
Súčin tretieho a druhého člena aritmetickej postupnosti je 3000. Ak je spoločný rozdiel 10, nájdite prvý člen. - MO Z9-I-6 2019
 Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami.
Kristína zvolila isté nepárne prirodzené číslo deliteľné tromi. Jakub s Dávidom potom skúmali trojuholníky, ktoré majú obvod v milimetroch rovný Kristínou zvolenému číslu a ktorých strany majú dĺžky v milimetroch vyjadrené navzájom rôznymi celými číslami. - Venček
 Na venček prišlo 12 chlapcov a 15 dievčat. Koľkými spôsobmi môžeme vybrať 4 tanečné páry?
Na venček prišlo 12 chlapcov a 15 dievčat. Koľkými spôsobmi môžeme vybrať 4 tanečné páry?
