Normálne rozloženie
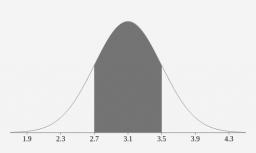
Na jednej strednej škole sú známky normálne distribuované s priemerom 3,1 a štandardnou odchýlkou 0,4. Aké percento študentov na vysokej škole majú známky medzi 2,7 a 3,5?
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom aritmetického priemeru?
Hľadáte štatistickú kalkulačku?
Hľadáte kalkulačku smerodajnej odchýlky?
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Chceš si dať zrátať kombinačné číslo?
Hľadáte štatistickú kalkulačku?
Hľadáte kalkulačku smerodajnej odchýlky?
Potrebujete pomôcť spočítať, vykrátiť či vynásobiť zlomky? Skúste našu zlomkovú kalkulačku.
Naša kalkulačka na výpočet percent Vám pomôže rýchlo vypočítať rôzne typické úlohy s percentami.
Chceš si dať zrátať kombinačné číslo?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Distribuovaná 6419
 Priemerná GPA (Grade Point Average = priemer známok) je 2,78 so štandardnou odchýlkou 0,45. Ak je GPA normálne distribuovaná, aké percento študentov má nasledujúce GPA? Vyriešte pomocou Z-skóre a nahláste príslušné percento: a. Menej ako 2,30 b. Menej ako
Priemerná GPA (Grade Point Average = priemer známok) je 2,78 so štandardnou odchýlkou 0,45. Ak je GPA normálne distribuovaná, aké percento študentov má nasledujúce GPA? Vyriešte pomocou Z-skóre a nahláste príslušné percento: a. Menej ako 2,30 b. Menej ako - Predpokladajme 80688
 Predpokladajme, že skóre v teste má normálne rozdelenie so strednou hodnotou X=74 a štandardnou odchýlkou s=18. Aké percento študentov má skóre vyššie ako 90? Aké percento študentov má skóre medzi 70 a 85? Dvadsať percent študentov robí lepšie, ako dosiah
Predpokladajme, že skóre v teste má normálne rozdelenie so strednou hodnotou X=74 a štandardnou odchýlkou s=18. Aké percento študentov má skóre vyššie ako 90? Aké percento študentov má skóre medzi 70 a 85? Dvadsať percent študentov robí lepšie, ako dosiah - Štandardnou 83165
 Skóre IQ je normálne rozdelené s priemerom 100 a štandardnou odchýlkou 15. Aké percento populácie má v IQ teste skóre vyššie ako 125?
Skóre IQ je normálne rozdelené s priemerom 100 a štandardnou odchýlkou 15. Aké percento populácie má v IQ teste skóre vyššie ako 125? - Predpokladajme 62904
 Predpokladajme, že pokojové pulzové frekvencie pre vzorku jednotlivcov sú normálne rozdelené s priemerom 70 a štandardnou odchýlkou 15. Na zistenie nasledujúcich veličín použite pravidlo 68-95-99,7. a. Percento pulzových frekvencií menej ako 70 b. percent
Predpokladajme, že pokojové pulzové frekvencie pre vzorku jednotlivcov sú normálne rozdelené s priemerom 70 a štandardnou odchýlkou 15. Na zistenie nasledujúcich veličín použite pravidlo 68-95-99,7. a. Percento pulzových frekvencií menej ako 70 b. percent
- Spravodlivých 80479
 Pri prijímacej skúške na vysokú školu sú účastníci hodnotení ako výborní, veľmi dobrí, dobrí a spravodliví. Zvážte, že skóre v skúške je normálne rozdelené s priemerom 78 a štandardnou odchýlkou 7,5. Účastníci, ktorí získajú prvých 5 % bodov, budú hodno
Pri prijímacej skúške na vysokú školu sú účastníci hodnotení ako výborní, veľmi dobrí, dobrí a spravodliví. Zvážte, že skóre v skúške je normálne rozdelené s priemerom 78 a štandardnou odchýlkou 7,5. Účastníci, ktorí získajú prvých 5 % bodov, budú hodno - Pravdepodobnosť 74714
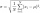 Váhy rýb v určitom jazere je normálne rozdelená s priemerom 11 lb (libier) a štandardnou odchýlkou 6 lb. Ak sú náhodne vybrané 4 ryby, aká je pravdepodobnosť, že priemerná hmotnosť bude medzi 8,6 a 14,6 lb? Vašu odpoveď zaokrúhlite na štvrté desatinné m
Váhy rýb v určitom jazere je normálne rozdelená s priemerom 11 lb (libier) a štandardnou odchýlkou 6 lb. Ak sú náhodne vybrané 4 ryby, aká je pravdepodobnosť, že priemerná hmotnosť bude medzi 8,6 a 14,6 lb? Vašu odpoveď zaokrúhlite na štvrté desatinné m - Štandardnou 82138
 Hmotnosť určitých druhov kapusty je bežne rozdelená s priemerom 1000 g a štandardnou odchýlkou 0,15 kg. V dávke 800 kusov kapusty odhadnite, koľko hmoty je medzi 750 g a 1290 g.
Hmotnosť určitých druhov kapusty je bežne rozdelená s priemerom 1000 g a štandardnou odchýlkou 0,15 kg. V dávke 800 kusov kapusty odhadnite, koľko hmoty je medzi 750 g a 1290 g. - Štandardizovaný
 Štandardizovaný test bol podaný tisícom študentov s priemerným skóre 85 a štandardnou odchýlkou 8. Náhodná vzorka 50 študentov dostala rovnaký test a vykázala priemerné skóre 83,20. Existujú dôkazy, ktoré preukazujú, že táto skupina má na úrovni 0,05 nižš
Štandardizovaný test bol podaný tisícom študentov s priemerným skóre 85 a štandardnou odchýlkou 8. Náhodná vzorka 50 študentov dostala rovnaký test a vykázala priemerné skóre 83,20. Existujú dôkazy, ktoré preukazujú, že táto skupina má na úrovni 0,05 nižš - Pravdepodobnosti 65614
 Hmotnosti žalúdka sú normálne rozdelené, s priemerom 1314 g a štandardnou odchýlkou 113 g. Uveďte pravdepodobnosť, že náhodne vybraný žalúdok váži viac ako 1118 g. (Vypočítajte pravdepodobnosti s použitím aspoň 4 desatinných miest. )
Hmotnosti žalúdka sú normálne rozdelené, s priemerom 1314 g a štandardnou odchýlkou 113 g. Uveďte pravdepodobnosť, že náhodne vybraný žalúdok váži viac ako 1118 g. (Vypočítajte pravdepodobnosti s použitím aspoň 4 desatinných miest. )
- Pravdepodobnosťou 82042
 Predpokladajme, že sa IQ v populácii riadi normálnym rozdelením so strednou hodnotou 100 bodov a štandardnou odchýlkou 10 bodov. S akou pravdepodobnosťou medzi 15 náhodne vybranými ľuďmi: a. Nie je nikto s IQ nad 130 bodov? b. Sú aspoň 2 ľudia s IQ nad 13
Predpokladajme, že sa IQ v populácii riadi normálnym rozdelením so strednou hodnotou 100 bodov a štandardnou odchýlkou 10 bodov. S akou pravdepodobnosťou medzi 15 náhodne vybranými ľuďmi: a. Nie je nikto s IQ nad 130 bodov? b. Sú aspoň 2 ľudia s IQ nad 13 - Predpokladajme 78684
 Predpokladajme, že výška chlapca je normálne rozdelená so strednou hodnotou 60 palcov a smerodajnou odchýlkou 10. Aké percento chlapcovej výšky by sme očakávali medzi 44 a 75, a menej ako 49 a 76 a viac?
Predpokladajme, že výška chlapca je normálne rozdelená so strednou hodnotou 60 palcov a smerodajnou odchýlkou 10. Aké percento chlapcovej výšky by sme očakávali medzi 44 a 75, a menej ako 49 a 76 a viac? - Pravdepodobnosť 30611
 Stoachy sú fiktívne bytosti vzdialene príbuzné bigfootovi a yetimu. Váhy stoacha sú normálne rozdelené, s priemerom 904 g a štandardnou odchýlkou 104 g. Uveďte pravdepodobnosť, že priemerná vzorka náhodnej vzorky s 36 hmotnosťami zásob presahuje 943 g. (U
Stoachy sú fiktívne bytosti vzdialene príbuzné bigfootovi a yetimu. Váhy stoacha sú normálne rozdelené, s priemerom 904 g a štandardnou odchýlkou 104 g. Uveďte pravdepodobnosť, že priemerná vzorka náhodnej vzorky s 36 hmotnosťami zásob presahuje 943 g. (U - Na strednej
 Na strednej škole v Lake High School je 3200 študentov a 3/8 z nich sú druháci. Ak sú 3/5 druhákov za vytvorenie tímu pre školu a 7/10 zostávajúcich študentov (nie druhákov) za vytvorenie tímu pre tím, koľko študentov je proti tejto myšlienke?
Na strednej škole v Lake High School je 3200 študentov a 3/8 z nich sú druháci. Ak sú 3/5 druhákov za vytvorenie tímu pre školu a 7/10 zostávajúcich študentov (nie druhákov) za vytvorenie tímu pre tím, koľko študentov je proti tejto myšlienke? - Štandardnou 8396
 Životnosť batérií má normálne rozloženie s priemerom 350 minút a štandardnou odchýlkou 10 minút. Aký dlho vydrží 68% batérií v minútach? Aký je životnosť v minútach, že približne 99,7 % batérií vydrží?
Životnosť batérií má normálne rozloženie s priemerom 350 minút a štandardnou odchýlkou 10 minút. Aký dlho vydrží 68% batérií v minútach? Aký je životnosť v minútach, že približne 99,7 % batérií vydrží?
- Štandardnou 72844
 Ročný plat odborníka na štatistiku na základnej úrovni (v tisícoch dolárov) je normálne rozdelený s priemerom 75 a štandardnou odchýlkou 12. X ∼ N ( μ = 75, σ = 12 ). Aká je minimálna mzda, na ktorú by sa mal špecialista štatistiky zamerať, aby zarobil
Ročný plat odborníka na štatistiku na základnej úrovni (v tisícoch dolárov) je normálne rozdelený s priemerom 75 a štandardnou odchýlkou 12. X ∼ N ( μ = 75, σ = 12 ). Aká je minimálna mzda, na ktorú by sa mal špecialista štatistiky zamerať, aby zarobil - Významnosti 49483
 Profesor na hodine strojopisu zistil, že priemerný výkon skúseného pisára je 85 slov za minútu. Náhodná vzorka 16 študentov absolvovala test na písanie a dosiahla sa priemernú rýchlosť 62 slov za minútu so štandardnou odchýlkou 8. Môžeme povedať, že výk
Profesor na hodine strojopisu zistil, že priemerný výkon skúseného pisára je 85 slov za minútu. Náhodná vzorka 16 študentov absolvovala test na písanie a dosiahla sa priemernú rýchlosť 62 slov za minútu so štandardnou odchýlkou 8. Môžeme povedať, že výk - Pravdepodobnosť 80803
 Zisk (alebo strata) z investície má normálne rozdelenie s priemerom 11 200 USD a štandardnou odchýlkou 8 250 USD. Aká je pravdepodobnosť, že dôjde skôr k strate ako k zisku?
Zisk (alebo strata) z investície má normálne rozdelenie s priemerom 11 200 USD a štandardnou odchýlkou 8 250 USD. Aká je pravdepodobnosť, že dôjde skôr k strate ako k zisku?
