Dokážte
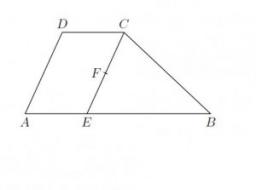
Lichobežník ABCD so základňami AB=a, CD=c má výšku v. Bod S je stred ramena BC. Dokážte že obsah trojuholníka ASD sa rovná polovici obsahu lichobežníka ABCD.
Zobrazujem 2 komentáre:
Žiak
staci ukazat (geometricky) ze presunom trojuhelniku DCS - stranou SC ku strane BS trojuhelnika ABS vznikne velky trojuhelnik s vyskou v, a stranou a+c. Jeho obsah je totozny s obsahem lichobezniku.
Žiak
Staci ukazat, ze zlepenim ABS a SCD tak ze B=C nam vznikne trojuholnik ADS (pretoze uhly Bega a Gama=180 stupnov) s polovicnou vyskou ako lichobeznik cize v/2. Cize obsah trojuholnika ADS je ((a+c)*v/2)/2=(a+c)*v/4 , co je presne polovica obsahu lichobeznika s obsahom (a+c)*v/2.
Tipy na súvisiace online kalkulačky
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Lichobežník
 Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm² a obsah trojuholníka DKC je 10 cm². Vypočítajte obsah lichobežníka ABCD.
Daný je lichobežník ABCD so základňami AB, CD. Nech K je stred strany AB a L je stred strany CD. Obsah trojuholníka ALB je 15 cm² a obsah trojuholníka DKC je 10 cm². Vypočítajte obsah lichobežníka ABCD. - Hranol - lichobežník
 Vypočítaj povrch štvorbokého hranola ABCDA'B'C'D 's lichobežníkovou podstavou ABCD. Výška hranola je 12 cm; údaje o lichobežníka ABCD: dĺžka základne AB je 8 cm, dĺžka základne CD je 3 cm, dĺžka ramena BC je 4 cm a dĺžka uhlopriečky AC je 7 cm. Napovieme:
Vypočítaj povrch štvorbokého hranola ABCDA'B'C'D 's lichobežníkovou podstavou ABCD. Výška hranola je 12 cm; údaje o lichobežníka ABCD: dĺžka základne AB je 8 cm, dĺžka základne CD je 3 cm, dĺžka ramena BC je 4 cm a dĺžka uhlopriečky AC je 7 cm. Napovieme: - Pravouhlý lichobežník
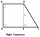 Pravouhlý lichobežník ABCD so základňami AB a CD je rozdelený uhlopriečkou AC na dva rovnoramené pravouhlé trojuholníky. Dĺžka uhlopriečky AC je rovná 62cm. Vypočítajte v cm štvorcových obsah lichobežníka a vypočítajte, o koľko cm sa líšia obvody trojuhol
Pravouhlý lichobežník ABCD so základňami AB a CD je rozdelený uhlopriečkou AC na dva rovnoramené pravouhlé trojuholníky. Dĺžka uhlopriečky AC je rovná 62cm. Vypočítajte v cm štvorcových obsah lichobežníka a vypočítajte, o koľko cm sa líšia obvody trojuhol - Lichobežník 4
 Vypočítajte veľkosť ramena b lichobežníka ABCD, ak a = 12 cm, c = 4 cm, d(AC)= d(BC) a obsah S(trojuholníka ABC) = 9 cm štvorcových.
Vypočítajte veľkosť ramena b lichobežníka ABCD, ak a = 12 cm, c = 4 cm, d(AC)= d(BC) a obsah S(trojuholníka ABC) = 9 cm štvorcových.
- Rovnoramennom 37621
 V rovnoramennom lichobežníku ABCD sú dané jeho základne AB=20cm, CD=12cm a ramená AD=BC=8cm. Určite jeho výšku a uhol alfa pri vrchole A
V rovnoramennom lichobežníku ABCD sú dané jeho základne AB=20cm, CD=12cm a ramená AD=BC=8cm. Určite jeho výšku a uhol alfa pri vrchole A - Rovnoramenný lichobežník 2
 Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných
Daný je rovnoramenný lichobežník ABCD, v ktorom platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho strane BC je bod K taký, že |BK| = 2|KC|, na jeho strane CD je bod L taký, že |CL|= 2|LD|, a na jeho strane DA je bod M taký, že|DM|= 2|MA|. Určte veľkosti vnútorných - V štvorci
 V štvorci ABCD so stranou a = 6 cm je bod E stred strany AB a bod F stred strany BC. Vypočítajte veľkosť všetkých uhlov trojuholníka DEF a dĺžky jeho strán.
V štvorci ABCD so stranou a = 6 cm je bod E stred strany AB a bod F stred strany BC. Vypočítajte veľkosť všetkých uhlov trojuholníka DEF a dĺžky jeho strán. - Štyri strany lichobežníka
 V lichobežníka ABCD je | AB | = 73,6 mm; | BC | = 57 mm; | CD | = 60 mm; | AD | = 58,6 mm. Vypočítajte veľkosti jeho vnútorných uhlov.
V lichobežníka ABCD je | AB | = 73,6 mm; | BC | = 57 mm; | CD | = 60 mm; | AD | = 58,6 mm. Vypočítajte veľkosti jeho vnútorných uhlov. - Trojuholník KLB
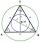 Daný je rovnostranný trojuholník ABC. Z bodu L ktorý je stredom strany BC tohto trojuholníka, je spustená kolmica k na stranu AB. Priesečník kolmice k a strany AB je označený ako bod K. Koľko % z obsahu trojuholníka ABC tvorí trojuholník KLB?
Daný je rovnostranný trojuholník ABC. Z bodu L ktorý je stredom strany BC tohto trojuholníka, je spustená kolmica k na stranu AB. Priesečník kolmice k a strany AB je označený ako bod K. Koľko % z obsahu trojuholníka ABC tvorí trojuholník KLB?
- Pre štvorciferné
 Pre štvorciferné číslo abcd platí, že ab : bc = 1 : 3 a bc : cd = 2 : 1 (ab, bc a cd sú dvojciferné čísla z cifier a, b, c, d). Určte toto číslo.
Pre štvorciferné číslo abcd platí, že ab : bc = 1 : 3 a bc : cd = 2 : 1 (ab, bc a cd sú dvojciferné čísla z cifier a, b, c, d). Určte toto číslo. - Vidieť harmonický
 Je pravda že veľkosť strednej priečky ľubovoľného lichobežníka je harmonickým priemerom veľkostí jeho základní? Dokážte to. Strednej priečka prechádza priesečníkom jeho uhlopriečok a je rovnobežná so základňami.
Je pravda že veľkosť strednej priečky ľubovoľného lichobežníka je harmonickým priemerom veľkostí jeho základní? Dokážte to. Strednej priečka prechádza priesečníkom jeho uhlopriečok a je rovnobežná so základňami. - Také tretinky
 Je daný lichobežníku ABCD s rovnobežnými stranami AB a CD pre bod E strany AB plati, že úsečka DE že delí lichobežník na dve časti s rovnakým obsahom. Spočítaj dĺžku úsečky AE.
Je daný lichobežníku ABCD s rovnobežnými stranami AB a CD pre bod E strany AB plati, že úsečka DE že delí lichobežník na dve časti s rovnakým obsahom. Spočítaj dĺžku úsečky AE. - Lichobežník - PU
 Parcela má tvar pravouhlého lichobežníka ABCD, kde ABIICD s pravým uhlom pri vrchole B. Strana AB má dĺžku 36 m. Dĺžky strán AB a BC sú v pomere 12:7. Dĺžky strán AB a CD sú v pomere 3:2 . Vypočítejte spotrebu pletiva na oplotenie parcely.
Parcela má tvar pravouhlého lichobežníka ABCD, kde ABIICD s pravým uhlom pri vrchole B. Strana AB má dĺžku 36 m. Dĺžky strán AB a BC sú v pomere 12:7. Dĺžky strán AB a CD sú v pomere 3:2 . Vypočítejte spotrebu pletiva na oplotenie parcely. - V lichobežníku
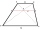 V lichobežníku ABCD sú dané základne: AB = 12cm CD = 4 cm A uhlopriečky sa pretínajú pod pravým uhlom. Aký je obsah tohto lichobežníka ABCD?
V lichobežníku ABCD sú dané základne: AB = 12cm CD = 4 cm A uhlopriečky sa pretínajú pod pravým uhlom. Aký je obsah tohto lichobežníka ABCD?
- Štvoruholník 14
 Daný je štvorec ABCD. Stred AB je E, stred BC je F, CD je G a stred DA je H. Spojíme AF, BG, CH a DE. Vo vnútri štvorca (približne v strede) priesečníky týchto úsečiek vytvoria štvoruholník. Vypočítajte obsah tohto štvoruholníka. Ďakujem
Daný je štvorec ABCD. Stred AB je E, stred BC je F, CD je G a stred DA je H. Spojíme AF, BG, CH a DE. Vo vnútri štvorca (približne v strede) priesečníky týchto úsečiek vytvoria štvoruholník. Vypočítajte obsah tohto štvoruholníka. Ďakujem - Plavecký bazén
 Plavecký bazén dlhý 30 metrov je naplnený vodou do hĺbky 1 metra na plytkom konci a 5 metrov na hlbokom konci a zvislej ploche bazéna má tvar lichobežníka s plochou danou S (abcd). = 1/2 (ab + cd) x ad. Aká je plocha prierezu abcd?
Plavecký bazén dlhý 30 metrov je naplnený vodou do hĺbky 1 metra na plytkom konci a 5 metrov na hlbokom konci a zvislej ploche bazéna má tvar lichobežníka s plochou danou S (abcd). = 1/2 (ab + cd) x ad. Aká je plocha prierezu abcd? - Lichobežník 7589
 Jeden lichobežník má AB=24M, BC=36M, CD=80M, DA=80M dlhé strany. Nájdite jeho obsah.
Jeden lichobežník má AB=24M, BC=36M, CD=80M, DA=80M dlhé strany. Nájdite jeho obsah.
